- MCC(Matthews Correlation Coefficient)とは何か
MCC(Matthews Correlation Coefficient)とは
MCCとは、
です。
正解のデータばかりで、誤ったデータが少ないようなときに利用できる指標です。
ちなみに、日本語ではマシューズ相関係数と呼びます。
計算式は以下の式で表されます。
$$MCC = \frac{TP×TN-FP×FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}$$
MCCは混同行列を使って計算されます。
この指標は-1~+1の範囲の値を取り、+1のときには完璧な予測をしていると判断します。
0のときにはランダムの予測をしているとし、-1のときには完全に逆の予測をしていると判断します。
MCCを計算してみる
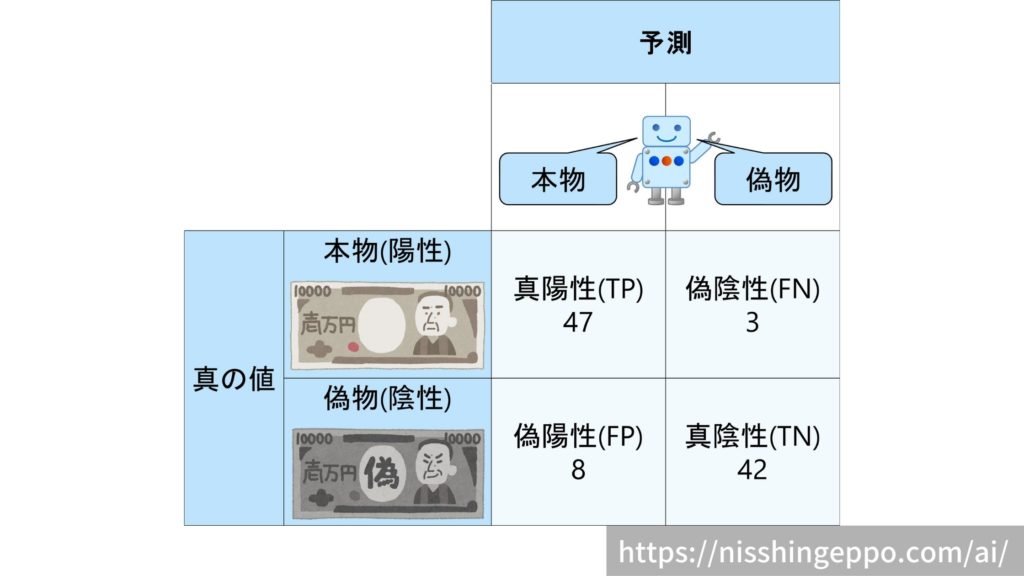
本物のお札50枚と偽物のお札50枚の計100枚のお札を判定する例を考えてみます。
均衡なデータ
本物と偽物を50枚ずつ使ったデータのときのMCCを計算してみます。
$$MCC = \frac{47×42-8×3}{\sqrt{(47+8)(47+3)(42+8)(42+3)}}=0.784$$
| MCC | accuracy | F1-score |
| 0.784 | 0.890 | 0.895 |
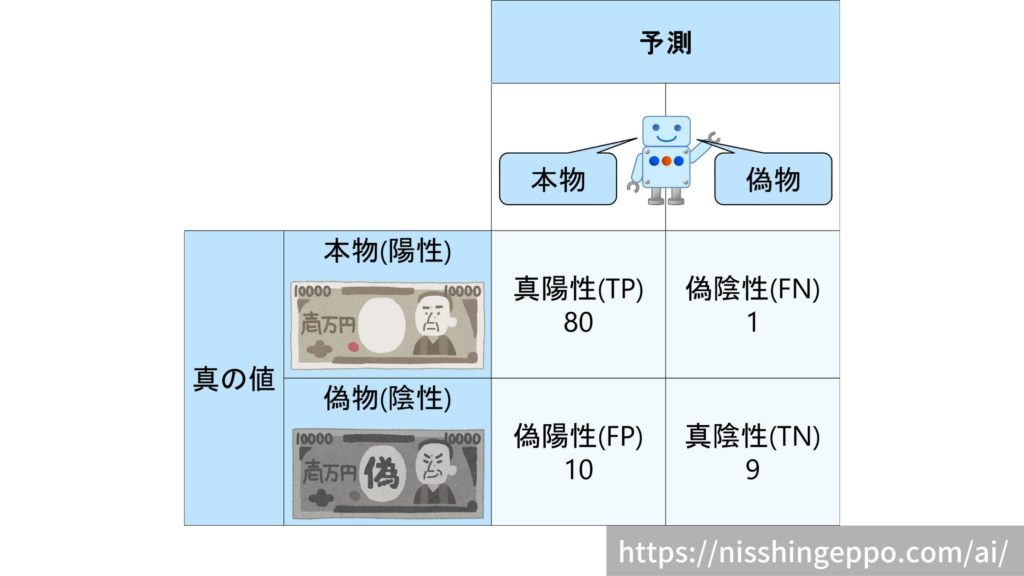
不均衡なデータ
本物が90枚で偽物を10枚という陽性に偏ったデータのときのMCCを計算してみます。
$$MCC = \frac{80×9 – 10×1}{\sqrt{(80+10)(80+1)(9+10)(9+1)}}=0.603$$
| MCC | accuracy | F1-score |
| 0.603 | 0.890 | 0.936 |
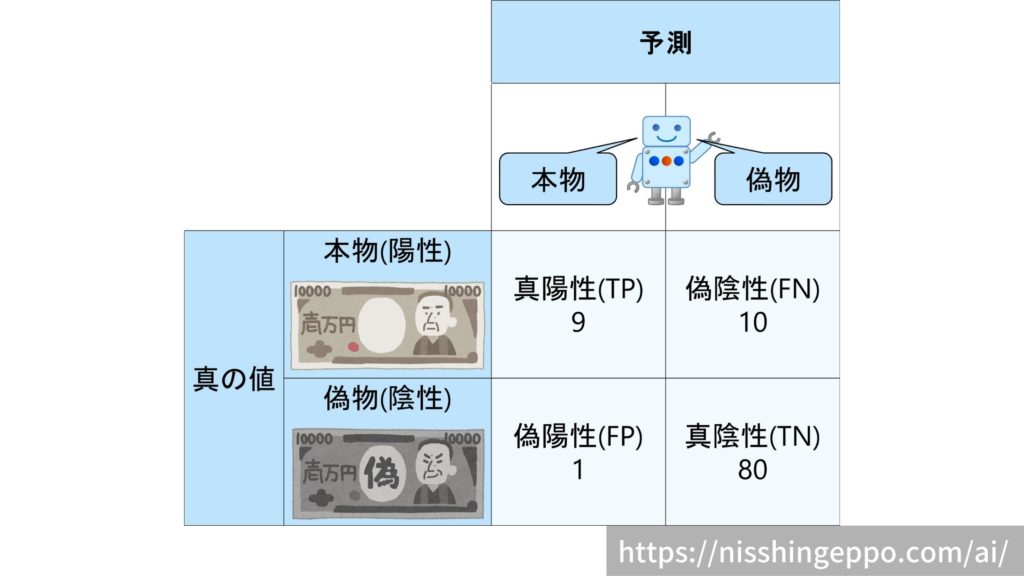
次に本物が10枚で偽物を90枚という陰性に偏ったデータのときのMCCを計算してみます。
予測結果は先程と全く逆になっただけなのでモデルの精度は変わっていません。
$$MCC = \frac{9×80 – 1×10}{\sqrt{(9+1)(9+10)(80+1)(80+10)}}=0.603$$
| MCC | accuracy | F1-score |
| 0.603 | 0.890 | 0.621 |
MCCでは正例が多い場合も負例が多い場合も結果は変わりません。
しかし、F値ではTNが考慮されないため負例が多い場合の精度が低くなってしまい、偏ったデータで正しく評価できていないことが分かります。
まとめ
MCCとは、機械学習モデルの評価指標の1つで、不均衡なデータに対して適切な評価をし易い指標です。
この指標は-1~+1の範囲の値を取り、+1のときには完璧な予測をしていると判断します。
0のときにはランダムの予測をしているとし、-1のときには完全に逆の予測をしていると判断します。






















コメント