- バイアス/バリアンスとは何か
- バイアス-バリアンス分解をする理由
- バイアス-バリアンス分解がやっていること
バイアス/バリアンスとは
バイアス/バリアンスとは、
です。
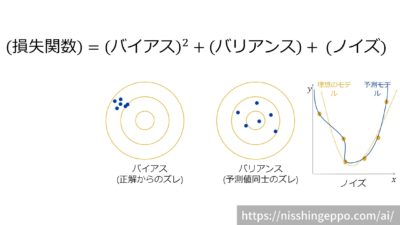
機械学習の予測に対する誤差(損失関数)の期待値は、以下のように3つの成分に分けることができます。
$$(損失関数の期待値)=(バイアス成分) + (バリアンス成分) + (ノイズ成分)$$
このように損失関数を「バイアス」「バリアンス」「ノイズ」に分解することをバイアス-バリアンス分解といいます。
次はそれぞれの要素について説明していきます。
バイアスとは
バイアスとは、
です。
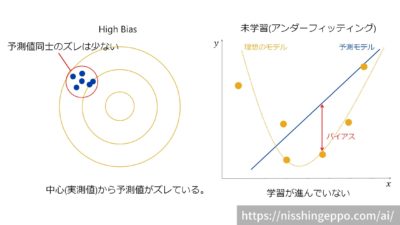
バイアスは予測値と実測値の差を表します。
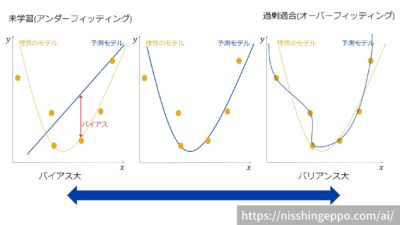
バイアスが高いと予測値が実測値から大きく離れてしまっています。
バイアスが大きければ、モデルは未学習状態(アンダーフィッティング)であると判断できます。
バリアンスとは
バリアンスとは、
です。
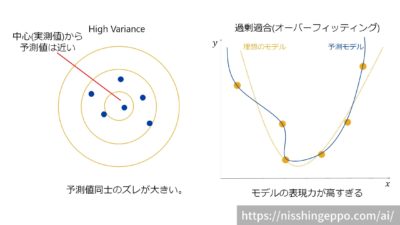
バリアンスは予測値の分散です。
バリアンスが高いとモデルの予測値同士が大きく散らばります。
バリアンスが大きいとモデルは過剰適合(オーバーフィッティング)であると判断できます。
ノイズとは
ノイズとは、
です。
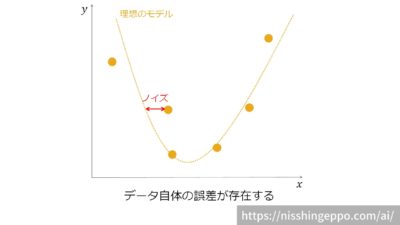
ノイズはデータを作成する時点で発生しています。
データ自体の誤差であるため、機械学習では学習することのできない部分となります。
どうしてバイアス-バリアンス分解をするのか
機械学習においてモデルの予測精度を高めるためには、損失関数を最小化する必要があります。
しかし、損失関数をそのまま使うと最小化を考えることが難しいので、バイアス-バリアンス分解を行って要素ごとに分解します。
ただし、バイアス-バリアンス分解ができるのは回帰タスク(二乗和誤差)のみ成立します。
バイアスとバリアンスはトレードオフ
機械学習モデルの精度を高めるためには、バイアスとバリアンスの両方を抑える必要があるのですが、この2つのはトレードオフの関係になっています。
バイアスを抑えようとするとバリアンスを大きくなってモデルの表現力が高くなりすぎてしまいます。
一方で、バリアンスを抑えようとするとバイアスが大きくなりモデルの表現力が下がってしまいます。
そのため、バイアスとバリアンスのバランスが取れたモデルが実用的なモデルとなります。
正則化などの手法を使って過剰適合を抑える(バリアンスを抑える)こともできます。
正則化についてはこちらの記事で説明をしています。
バイアス-バリアンス分解を数式で説明
まず、損失関数(二乗誤差の期待値)を数式で表してみましょう。
変数は以下のように定義します。
$$D:データ集合、x:説明変数、y(x):予測モデル\\h(x):理想的な予測モデル、t:目的変数(実データの値)、E:期待値$$
すると損失関数は、このように表すことができます。
$$(損失関数)=第1項(予測値と理想値の差) + 第2項(理想値と実データの差)$$
$$E\left( L\right) =\int \left\{ y\left( x\right) -h\left( x\right) \right\} ^{2}p\left( x\right) dx + \int \int \left\{ h\left( x\right) -t\right\} ^{2}p\left( x,t\right) dxdy$$
第2項は理想値(完璧なモデルの予測値)と実データの差を表す項なので、つまりノイズを表しています。
第1項は更に展開することができて、以下のような式で表されます。
$$損失関数の第1項(予測値と理想値の差) = バイアス + バリアンス$$
$$\int \left\{ y\left( x\right) -h\left( x\right) \right\} ^{2}p\left( x\right) dx =
\\\int \left\{ E_{D}\left[ y\left( x;D\right) \right] -h\left( x\right) \right\} ^{2}p(x)dx +
\int E_{D}\left[ \left\{ y\left( x;D\right) -E_{D},\left[ y\left( x;D\right) \right] \right\} ^{2}\right] p\left( x\right) dx$$
バイアスの式では、予測値の平均が理想値からどれくらい離れているかを表しています。
バリアンスの式では、特定のデータが予測値全体からどれくらい離れているかを表しています。
これまでの数式をまとめると、以下のように整理できます。
$$(バイアス)^{2}=\int \left\{ E_{D}\left[ y\left( x;D\right) \right] -h\left( x\right) \right\} ^{2}p(x)dx $$
$$(バリアンス)=\int E_{D}\left[ \left\{ y\left( x;D\right) -E_{D},\left[ y\left( x;D\right) \right] \right\} ^{2}\right] p\left( x\right) dx$$
$$(ノイズ)=\int \int \left\{ h\left( x\right) -t\right\} ^{2}p\left( x,t\right) dxdy$$
まとめ
バイアス/バリアンスとは、機械学習の誤差(損失関数)を分解した成分です。
損失関数はバイアス-バリアンス分解することで、「バイアス」「バリアンス」「ノイズ」に分解することができます。
機械学習モデルの精度を高めるためには、バイアスとバリアンスの両方を抑える必要があるのですが、この2つのはトレードオフの関係になっています。






















コメント