カーネル法(Kernel method)とは？次元を変えて分かりやすくするテクニック!!

この記事を読んで分かること

カーネル法(Kernel method)とは何か
カーネル関数の種類
カーネル法を用いたサポートベクターマシンのpythonでの実装

カーネル法(Kernel method)とは?
カーネル関数の種類
カーネル法をpythonで実装
まとめ

カーネル法(Kernel method)とは?

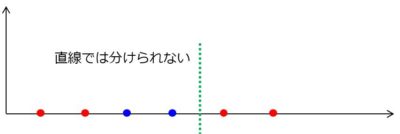
カーネル法とは、データを変換して(データの次元を上げて)分析しやすくする手法です。例えば、下の図のような直線的な赤と青のデータが有り、これを直線で分離させようとしてもできません。

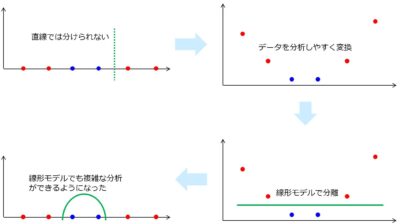
ここで、1次元のデータから2次元のデータに次元を上げてみます。図では各値にの2乗をとったイメージをしています。すると、線形分離(直線で分離)が可能になりました。

このカーネル法という考え方を使うことで、線形なモデルを利用することができるようになります。

わざわざ線形なモデルを使わなくてもいいのではないかと疑問に思うかもしれませんが、次元の高いモデルを使うと、汎化性能が低くなってしまったりしてデータ分析が難しくなります。

このように、分析したいデータの次元数を上げて単純な形に変えることでデータ分析しやすくなることをカーネルトリックと言います。

カーネル法を使うことで複雑なデータに対して人間が特徴量を作らなくても分析することができるようになりました。

カーネル法を利用すると特徴量が何であるかを知ることはできなくなります。カーネル法は、特徴量との相関よりも精度が要求される場合に利用します。

ロボくん

機械学習で使われるカーネルは写像で、次元を変えるという意味合いで使われているよ。同じ単語でもOSのカーネルとは別物なんだね!!

カーネル関数の種類

カーネル法で利用できるカーネル関数には様々な種類があります。もちろん利用するカーネル関数によって得られる決定境界の様子は変わります。代表的なカーネル関数として以下ようなものがあります。


カーネル関数	カーネル関数の数式
線形カーネル	$$K(x_i,x_j)=x_i・x_j$$
シグモイドカーネル	$$K(x_i,x_j)=tanh(b{x_i}^Tx_j + c)$$
多項カーネル	$$K(x_i,x_j)=({x_i}^Tx_j + c)^d$$
ガウスカーネル	$$K(x_i,x_j)=e^{-\frac{{￨￨x_i – x_j￨￨}^2}{2σ^2}}$$
RBFカーネル	$$K(x_i,x_j)=e^{-γ{￨￨x_i – x_j￨￨}^2}$$

カーネル法をpythonで実装

カーネル法をサポートベクターマシンと組み合わせて学習した例をpythonで実装してみました。機械学習のライブラリであるsklearnを用い、カーネル関数はデフォルトのRBF(Radial Basis Function)を使用します。

必要ライブラリのインポート

import matplotlib.pyplot as plt
import numpy as np

from sklearn.svm import SVC
from sklearn.datasets import make_gaussian_quantiles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

データの生成

#データ生成
X, y = make_gaussian_quantiles(n_features=2, n_classes=2, n_samples=300)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

#データの色分け
X_blue = X[y==0,:] X_red = X[y==1,:]

サポートベクターマシンのモデルで学習する

#サポートベクターマシン(カーネル法)で分類する
model = SVC()
model.fit(X_train, y_train)#学習
y_pred = model.predict(X_test)#推定
accuracy_score(y_pred, y_test)#正解率

ちなみに、今回のテストデータでは正解率は90%となりました。

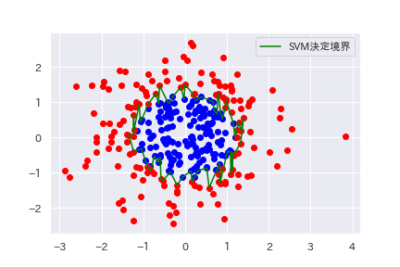
結果の表示

# 決定境界の描画の準備
line = model.support_vectors_#決定境界線
line_u = line[line[:,1] > 0,:]
line_d = line[line[:,1] <= 0,:]
line_u = line_u[np.argsort(line_u[:,0]),:]
line_d = line_d[np.argsort(-line_d[:,0]),:]
l = np.concatenate([line_u,line_d])
l = np.concatenate([l,[l[0,:]]])

#結果の描画
plt.scatter(X_blue[:,0],X_blue[:,1],c="blue")
plt.scatter(X_red[:,0],X_red[:,1],c="red")

plt.plot(l[:,0],l[:,1],c=”green”,label=”SVM決定境界”)
plt.legend()

サポートベクターマシンの決定境界が線形ではなく複雑な形になり、データが綺麗に分類されていることが分かります。

ロボくん

ディープラーニングが登場する前には、カーネル法を用いたサポートベクターマシンは人気のある手法だったんだよ。

まとめ

カーネル法とは何かをまとめると以下の3つの特徴を持つテクニックです。

データを変換して(データの次元を上げて)分析しやすくするテクニック
複雑なデータに対して人間が特徴量を作らなくても分析することができる
一般化線形モデルと組み合わせて利用すると効果的