【線形代数】特異値分解とは?例題付きで分かりやすく解説!!

この記事を読んで分かること

特異値分解とは何か
特異値分解をするメリット
特異値分解の求め方

特異値分解とは
特異値分解のメリット
特異値分解の求め方
特異値分解の具体例
まとめ
参考文献

特異値分解とは

特異値分解とは、

ある行列を直交行列と対角行列の積に分解する計算のこと

です。

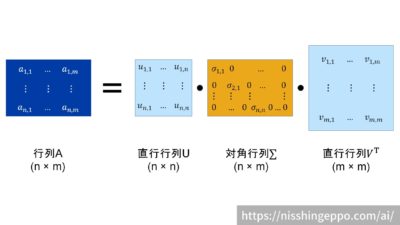
$$A = U∑V^{T}$$のような数式で表されます。

言葉だけだとわかりにくいですが、以下の図のようなイメージです。

数式にするとこのように表されます。

$A = U∑V^{T} \\
\quad= \left(\begin{array}{cccc}\vec{u_{1}} & \vec{u_{2}} & \ldots & \vec{u_{n}}\end{array}\right)\left(
\begin{array}{cccc}
λ_{1} & 0 & \ldots & 0 \\
0 & λ_{2} & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & λ_{n}
\end{array}
\right)\left(\begin{array}{cccc}\vec{v_{1}} & \vec{v_{2}} & \ldots & \vec{v_{n}}\end{array}\right)^{T}$

$U$の成分である$\vec{u_{n}}$は左特異ベクトルと呼び、

$V$の成分である$\vec{v_{n}}$は右特異ベクトルと呼びます。

特異値分解された後は3つの行列になり、それぞれこのような性質を持ちます。

特異値分解後の行列

$U : 直交行列$
$∑ : 対角行列$
$V : 直交行列$

行列$U$と$V$は直行行列であるため、

$$UU^{T}=U^{T}U=I $$
$$VV^{T}=V^{T}V=I$$

が成り立ちます。

また、特異値分解は行列の形によらず行うことができます。

対角化では正方行列にしか適用できなかったので、特異値分解は適用範囲が広いことも特徴の1つです。

特異値分解のメリット

特異値分解について知ることができたと思いますが、どうしてこんなことをするのか疑問に思った方もいるかもしれません。

特異値分解するメリットの一つとして、

行列の累乗を計算するのが簡単になる

ということが挙げられます。

特異値分解の求め方

行列$A$を特異値分解するためには、まず$AA^{T} $を計算します。

行列$U$と$V$は直行行列であるので、以下のようになり、

$$ AA^{T} = U∑V^{T}V∑^{T}U^{T}$$

$$ AA^{T} = U∑∑^{T}U^{T}$$

$AA^{T}$は正方行列なので、この式に対して対角化を行うことができます。

$AA^{T}$の固有値を求めると、

$$ AA^{T}\vec{x} = λ\vec{x}$$

$$ (AA^{T}-λI)\vec{x} = \vec{0} $$

となり、この固有ベクトルを並べたものが、$U$となります。

$$U=\left(\begin{array}{cccc}\vec{u_{1}} & \vec{u_{2}} & \ldots & \vec{u_{n}}\end{array}\right)$$

ただし、$\vec{u_{n}}$は単位ベクトルとします。

続いて行列$V$の行列を求めていきます。

$AA^{T} $を計算し、先程の行列$U$と同様の考え方をしていきます。

$$ A^{T} A= V∑U^{T}U∑^{T}V^{T}$$

$$ A^{T} A = V∑∑^{T}V^{T}$$

$A^{T}A$も正方行列なので、この式に対して対角化を行うことができます。

$A^{T}A$の固有値を求め、

$$ A^{T}A\vec{x} = λ\vec{x}$$

$$ (A^{T}A-λI)\vec{x} = \vec{0} $$

この固有ベクトルを並べたものが、$V$となります。

$$V=\left(\begin{array}{cccc}\vec{v_{1}} & \vec{v_{2}} & \ldots & \vec{v_{n}}\end{array}\right)$$

ただし、$\vec{v_{n}}$は単位ベクトルとします。

次に対角行列$∑$を求めていきます。

$∑$の成分は、$AA^{T}$の固有値から求めることができ、

$$\sigma =\sqrt{λ}$$

という関係式が成り立ちます。

固有値を並べた対角行列は、

$$ ∑∑^{T}=\left(
\begin{array}{cccccc}
σ_{1} & 0 & \ldots & 0 & \ldots & 0 \\
0 & σ_{2} & \ldots & 0 & \ldots & 0\\
\vdots & \vdots & \ddots & \vdots & \vdots & \vdots\\
0 & 0 & \ldots & σ_{n} & \ldots & 0
\end{array}
\right)
\left(
\begin{array}{cccc}
σ_{1} & 0 & \ldots & 0 \\
0 & σ_{2} & \ldots & 0\\
\vdots & \vdots & \ddots & \vdots\\
0 & 0 & \ldots & σ_{n}\\
\vdots & \vdots & \vdots & \vdots\\
0 & \ldots & \ldots & 0
\end{array}
\right)\\
=\left(
\begin{array}{cccc}
σ_{1}^{2} & 0 & \ldots & 0 \\
0 & σ_{2}^{2} & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & σ_{n}^{2}
\end{array}
\right) \\=\left(
\begin{array}{cccc}
λ_{1} & 0 & \ldots & 0 \\
0 & λ_{2} & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & λ_{n}
\end{array}
\right)$$

このとき、$σ$は大きいものから順に並べます。

以上で、行列$U,∑,V$をすべて求めることができました。

特異値分解の具体例

では、実際に問題を解いてみましょう。

問題

$ A = \left(
\begin{array}{ccc}
2 & 1 & 1 \\
1 & 1 & 2 \\
\end{array}
\right)$を$A=UDV^{T}$という形に特異値分解をしなさい。

まずは、$AA^{T}$を求めます。

$AA^{T} = \left(
\begin{array}{ccc}
2 & 1 & 1 \\
1 & 1 & 2 \\
\end{array}
\right)\left(
\begin{array}{cc}
2 & 1 \\
1 & 1 \\
1 & 2
\end{array}
\right) \\
\qquad=\left(
\begin{array}{cc}
6 & 5 \\
5 & 6
\end{array}
\right)
$

次に、$AA^{T}$の対角化を行うため、固有値・固有ベクトルを求めます。

$
|AA^{T} – λE| = 0\\
(6-λ)^{2} – 25 = 0\\
λ^{2} – 12λ + 11 = 0\\
(λ – 11)(λ – 1) = 0\\
λ = 11,\quad1
$

それぞれの固有値に対応する固有ベクトルを求めていきます。

i) λ = 11のとき

$
(AA^{T} – λE)\vec{u_{1}} = \vec{0}\\
\left(\begin{array}{cc}
-5 & 5 \\
5 & -5
\end{array}
\right)\vec{u_{1}} = \vec{0}\\
\left(\begin{array}{cc}
1 & -1 \\
0 & 0
\end{array}
\right)\vec{u_{1}} = \vec{0}\\
\vec{u_{1}} = \left(\begin{array}{c}
1 \\
1
\end{array}
\right)s_{1}
$

ii) λ = 1のとき

$
(AA^{T} – λE)\vec{u_{2}} = \vec{0}\\
\left(\begin{array}{cc}
5 & 5 \\
5 & 5
\end{array}
\right)\vec{u_{2}} = \vec{0}\\
\left(\begin{array}{cc}
1 & 1 \\
0 & 0
\end{array}
\right)\vec{u_{2}} = \vec{0}\\
\vec{u_{2}} = \left(\begin{array}{c}
1 \\
-1
\end{array}
\right)s_{2}
$

$\vec{u}$は単位行列であるので、ノルムを1にすると

$
U=\left(\begin{array}{cc}\vec{u_{1}} & \vec{u_{2}} \end{array}\right)\\
\quad=\left(\begin{array}{cc}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{array}\right)
$

固有値から$∑$を求めます。

$
∑∑^{T} = \left( \begin{array}{cc}
λ_{1} & 0 \\
0 & λ_{2}
\end{array} \right)\\
\left( \begin{array}{ccc}
σ_{1} & 0 & 0\\
0 & σ_{2}& 0
\end{array} \right)
\left( \begin{array}{cc}
σ_{1} & 0\\
0 & σ_{2}\\
0 & 0
\end{array} \right)
=\left( \begin{array}{cc}
λ_{1} & 0 \\
0 & λ_{2}
\end{array} \right)\\
\left( \begin{array}{cc}
σ_{1}^{2} & 0 \\
0 & σ_{2}^{2}
\end{array} \right)=\left( \begin{array}{cc}
11 & 0 \\
0 & 1
\end{array} \right)\\
σ_{1} = \sqrt{11}, \quadσ_{2} =1
$

$
∑ = \left( \begin{array}{ccc}
\sqrt{11} & 0 & 0\\
0 & 1 & 0
\end{array} \right)
$

続いて$V$を求めるために固有値が必要になリますが、$∑$から導出できます。

$
∑^{T}∑ = \left( \begin{array}{ccc}
λ_{1} & 0 & 0\\
0 & λ_{2} & 0\\
0 & 0 & λ_{3}
\end{array} \right)\\
\left( \begin{array}{cc}
σ_{1} & 0\\
0 & σ_{2}\\
0 & 0
\end{array} \right)
\left( \begin{array}{ccc}
σ_{1} & 0 & 0\\
0 & σ_{2}& 0
\end{array} \right)
=\left( \begin{array}{ccc}
λ_{1} & 0 & 0\\
0 & λ_{2} & 0\\
0 & 0 & λ_{3}
\end{array} \right)\\
\left( \begin{array}{ccc}
σ_{1}^{2} & 0 & 0 \\
0 & σ_{2}^{2} & 0 \\
0 & 0 &0
\end{array} \right)
=\left( \begin{array}{ccc}
λ_{1} & 0 & 0\\
0 & λ_{2} & 0\\
0 & 0 & λ_{3}
\end{array} \right)\\
λ_{3} = 0
$

$A^{T}A$に対して、それぞれの固有値に対応する固有ベクトルを求めていきます。

$AA^{T} = \left(
\begin{array}{cc}
2 & 1 \\
1 & 1 \\
1 & 2
\end{array}
\right)\left(
\begin{array}{ccc}
2 & 1 & 1 \\
1 & 1 & 2 \\
\end{array}
\right)\\
\qquad=\left(
\begin{array}{ccc}
5 & 3 & 4 \\
3 & 2 & 3 \\
4 & 3 & 5 \\
\end{array}
\right)
$

i) λ = 11のとき

$
(AA^{T} – λE)\vec{v_{1}} = \vec{0}\\
\left(\begin{array}{ccc}
-6 & 3 & 4 \\
3 & -9 & 3 \\
4 & 3 & -6
\end{array}
\right)\vec{v_{1}} = \vec{0}\\
\left(\begin{array}{ccc}
1 & 0 & -1 \\
0 & 3 & -2 \\
0 & 0 & 0
\end{array}
\right)\vec{v_{1}} = \vec{0}\\
\vec{v_{1}} = \left(\begin{array}{c}
3 \\
2 \\
3
\end{array}
\right)t_{1}
$

ii) λ = 1のとき

$
(AA^{T} – λE)\vec{v_{2}} = \vec{0}\\
\left(\begin{array}{ccc}
4 & 3 & 4 \\
3 & 1 & 3 \\
4 & 3 & 4
\end{array}
\right)\vec{v_{2}} = \vec{0}\\
\left(\begin{array}{ccc}
1 & 0 & 1 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{array}
\right)\vec{v_{2}} = \vec{0}\\
\vec{v_{2}} = \left(\begin{array}{c}
1 \\
0 \\
-1
\end{array}
\right)t_{2}
$

iii) λ = 0のとき

$
(AA^{T} – λE)\vec{v_{3}} = \vec{0}\\
\left(\begin{array}{ccc}
5 & 3 & 4 \\
3 & 2 & 3 \\
4 & 3 & 5
\end{array}
\right)\vec{v_{3}} = \vec{0}\\
\left(\begin{array}{ccc}
1 & 0 & -1 \\
0 & 1 & 3 \\
0 & 0 & 0
\end{array}
\right)\vec{v_{3}} = \vec{0}\\
\vec{v_{3}} = \left(\begin{array}{c}
1 \\
-3 \\
1
\end{array}
\right)t_{3}
$

$\vec{v}$は単位行列であるので、ノルムを1にすると

$
V=\left(\begin{array}{cc}\vec{v_{1}} & \vec{v_{2}} & \vec{v_{3}}\end{array}\right)\\
\quad=\left(\begin{array}{ccc}
\frac{3}{\sqrt{22}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{11}} \\
\frac{2}{\sqrt{22}} & 0 & -\frac{3}{\sqrt{11}} \\
\frac{3}{\sqrt{22}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{11}}
\end{array}\right)
$

よって

$
A = \left(\begin{array}{cc}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{array}\right)
\left( \begin{array}{ccc}
\sqrt{11} & 0 & 0\\
0 & 1 & 0
\end{array} \right)
\left(\begin{array}{ccc}
\frac{3}{\sqrt{22}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{11}} \\
\frac{2}{\sqrt{22}} & 0 & -\frac{3}{\sqrt{11}} \\
\frac{3}{\sqrt{22}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{11}}
\end{array}\right)^{T}
$