【線形代数】固有値・固有ベクトルとは?例題付きで分かりやすく解説!!

この記事を読んで分かること

固有値・固有ベクトルとは何か
固有値・固有ベクトルの求め方

固有値・固有ベクトルとは
固有値・固有ベクトルの求め方
固有値・固有ベクトル導出の具体例
まとめ
参考文献

固有値・固有ベクトルとは

固有値とは、

ある正方行列$A$に対して、$A\vec{x} = λ\vec{x}$の式を満たすときの$λ$のこと

です。

固有値ベクトルとは、

ある正方行列$A$に対して、$A\vec{x} = λ\vec{x}$の式を満たすときの$\vec{x}$のこと

です。

$$ A\vec{x} = λ\vec{x}$$

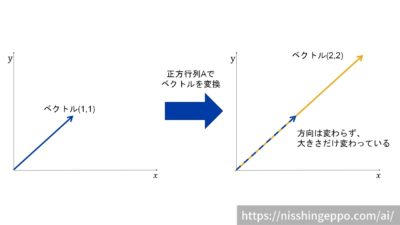
というのは、あるベクトルに正方行列(A)を掛けても方向が変わらず、大きさだけが変わるような変換をすることを表しています。

この図の場合では、固有ベクトル$x$は(1,1)で、固有値$λ$は2となります。

正方行列に対して固有値・固有ベクトルはセットなりますが、全ての正方行列に存在するわけではありません。

固有ベクトルは、以下を満たすことが条件となっています。

$\vec{x}$が$\vec{0}$でない

0ベクトルの場合だとどんな行列にも成り立ってしまうので、当然の制約ですね。

固有値・固有ベクトルの求め方

まず、固有値・固有ベクトルの定義を式変形します。

$$ A\vec{x} = λ\vec{x}$$

$$ (A-λE)\vec{x} = \vec{0} $$

ここで、固有ベクトルの条件を思い出すと、

固有ベクトルの条件

$\vec{x}$が0ベクトルでない

$⇔ (A-λE)$が逆行列を持たない

$⇔det(A-λE) = 0$

が導出されます。

$$ det(A-λI) = 0$$

は特性方程式と呼ばれ、この式を満たすλ(固有値)を探していきます。

そして、求めた固有値を元の式

$$ (A-λI)\vec{x} = \vec{0} $$

に代入して、固有ベクトル$\vec{x} $を導出することができます。

固有値・固有ベクトル導出の具体例

では、実際に問題を解いてみましょう。

問題

$A = \left(\begin{array}{cc}
1 & 2 \\
3 & 2 \\
\end{array}
\right)$
の固有値と固有値ベクトルを求めよ

まずは$det(A-λE) = 0 $となる固有値λを求めます。

$
det(A-λE) = 0 \\
\left|\begin{array}{cc}
1-λ & 2 \\
3 & 2-λ \\
\end{array}
\right| = 0\\
(λ^{2}-3λ+2)-6 = 0\\
(λ-4)(λ+1)=0\\
λ=4, \quad-1
$

それぞれの固有値に対応する固有ベクトル$\vec{x} $を求めます。

i) λ=4のとき

$
(A-λE)\vec{x_{1}} = \vec{0} \\
\left(\begin{array}{cc}
-3 & 2 \\
3 & -2 \\
\end{array}
\right)\vec{x_{1}} = \vec{0}\\
\left(\begin{array}{cc}
3 & -2 \\
0 & 0 \\
\end{array}\right)\vec{x_{1}} = \vec{0}\\
\vec{x_{1}} = \left(\begin{array}{c}
2 \\
3 \\
\end{array}
\right)t_{1}
$

ii) λ=-1のとき

$
(A-λE)\vec{x_{2}} = \vec{0} \\
\left(\begin{array}{cc}
2 & 2 \\
3 & 3 \\
\end{array}
\right)\vec{x_{2}} = \vec{0}\\
\left(\begin{array}{cc}
1 & 1 \\
0 & 0 \\
\end{array}\right)\vec{x_{2}} = \vec{0}\\
\vec{x_{2}} = \left(\begin{array}{c}
1 \\
-1 \\
\end{array}
\right)t_{2}
$