- 対角化とは何か
- 対角化をするメリット
- 対角化のやり方
対角化とは
対角化とは、
です。
$$P^{-1}AP= D$$のような数式で表されます。
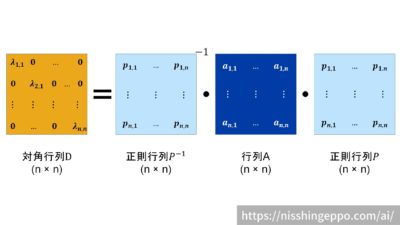
言葉だけだとわかりにくいですが、以下の図のようなイメージです。
数式にするとこのように表されます。
$$D = P^{-1}AP $$
$$\left(
\begin{array}{cccc}
λ_{1} & 0 & \ldots & 0 \\
0 & λ_{2} & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & λ_{n}
\end{array}
\right)=
P^{-1}AP
$$
対角化された後は3つの行列が登場し、それぞれこのような性質を持ちます。
\(P\)は正則行列であるため、
$$PP^{-1}=P^{-1}P=E $$
が成り立ちます。
また、対角化は正方行列にしか行うことができません。
正方行列でない行列に対して対角行列を導出する方法として、特異値分解という手法も存在します。
この記事では詳しく解説しませんが、気になる人はこちらの記事も合わせて読んでみてください。

対角化のメリット
対角化について知ることができたと思いますが、どうしてこんなことをするのか疑問に思った方もいるかもしれません。
対角化するメリットの一つとして、
ということが挙げられます。
\(A^n\)を求めたいときには、
\(P^{-1}AP = D \)と対角化します。
対角行列の累乗は各成分の累乗であることを利用すると簡単に計算することができます。
\(D^{n} =
\left(
\begin{array}{cccc}
λ_{1}^{n} & 0 & \ldots & 0 \\
0 & λ_{2}^{n} & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & λ_{n}^{n}
\end{array}
\right)
\)
\(D^2 = P^{-1}APP^{-1}AP \\
D^2=P^{-1}A^2P \\
PD^2P^{-1}=A^2\)
となり、この性質を利用すると
\(A^n = PD^n P^{-1} \)
となります。
こうして行列Aの累乗を簡単に行うことができます。
行列の累乗は、ディープラーニングで同じ層を重ねたときの計算など頻繁に出てくるので非常に有用です。
対角化の求め方
行列\(A\)を対角化するためには、まず固有値\(λ\)と固有ベクトル\( \vec{v}\)を求めます。
固有値・固有ベクトルについてはこちらの記事で詳しく説明しています。

求めた固有ベクトルを並べたものが正則行列\(P\)になります。
$$P=\left(\begin{array}{cccc}\vec{v_{1}} & \vec{v_{2}} & \ldots & \vec{v_{n}}\end{array}\right)$$
正則行列\(P\)が求まったので、掃き出し法などを使い逆行列\(P^{-1}\)が求められます。
また、対角化された行列\(D\)は固有値を並べた行列となります。
$$D = \left(\begin{array}{cccc}
λ_{1} & 0 & \ldots & 0 \\
0 & λ_{2} & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & λ_{n}
\end{array}
\right)$$
以上で、行列\(P,D,P^{-1}\)をすべて求めることができました。
対角化の具体例
では、実際に問題を解いてみましょう。
\(A = \left(\begin{array}{cc}
1 & 2 \\
3 & 2 \\
\end{array}
\right)\)を対角化しなさい。
まずはAの固有値と固有ベクトルを求めます。
\(
det(A-λE) = 0 \\
\left|\begin{array}{cc}
1-λ & 2 \\
3 & 2-λ \\
\end{array}
\right| = 0\\
(λ^{2}-3λ+2)-6 = 0\\
(λ-4)(λ+1)=0\\
λ=4, \quad-1
\)
それぞれの固有値に対応する固有ベクトル\(\vec{x} \)を求めます。
i) λ=4のとき
\(
(A-λE)\vec{x_{1}} = \vec{0} \\
\left(\begin{array}{cc}
-3 & 2 \\
3 & -2 \\
\end{array}
\right)\vec{x_{1}} = \vec{0}\\
\left(\begin{array}{cc}
3 & -2 \\
0 & 0 \\
\end{array}\right)\vec{x_{1}} = \vec{0}\\
\vec{x_{1}} = \left(\begin{array}{c}
2 \\
3 \\
\end{array}
\right)t_{1}
\)
ii) λ=-1のとき
\(
(A-λE)\vec{x_{2}} = \vec{0} \\
\left(\begin{array}{cc}
2 & 2 \\
3 & 3 \\
\end{array}
\right)\vec{x_{2}} = \vec{0}\\
\left(\begin{array}{cc}
1 & 1 \\
0 & 0 \\
\end{array}\right)\vec{x_{2}} = \vec{0}\\
\vec{x_{2}} = \left(\begin{array}{c}
1 \\
-1 \\
\end{array}
\right)t_{2}
\)
固有値と固有ベクトルを求めることができました。
\(
λ_{1}=4, \quad\vec{v_{1}} = \left(\begin{array}{c}
2 \\
3 \\
\end{array}
\right)\\
λ_{2}=-1, \quad\vec{v_{2}} = \left(\begin{array}{c}
1 \\
-1 \\
\end{array}
\right)
\)
固有値から対角行列\(D\)は、
\(
D=\left(\begin{array}{cc}
4 & 0 \\
0 & -1 \\
\end{array}
\right)
\)
となります。
固有ベクトルからPは、
\(
P=\left(\begin{array}{cc}
2 & 1\\
3 & -1 \\
\end{array}
\right)
\)
となります。
Pの逆行列を掃き出し法などで求めます。
\(
P^{-1}=\frac{1}{5} \left(\begin{array}{cc}
1 & 1 \\
3 & -2 \\
\end{array}
\right)
\)
よって、
\(
P^{-1}AP=\left(\begin{array}{cc}
4 & 0 \\
0 & -1 \\
\end{array}
\right)
\)
と対角化することができました。
まとめ
対角化とは、ある正方行列\(A\)を正則行列\(P\)を使って、対角行列\(D\)に変換することです。
$$D = P^{-1}AP $$のような数式で表されます。
行列\(A\)を対角化するためには、まず\(A\)の固有値と固有ベクトルを計算することで求めます。
対角化するメリットの一つとして、行列の累乗を計算するのが簡単になることが挙げられますが、対角化は正方行列にしか適用できません。






















コメント