- シグモイド関数とは何か
- シグモイド関数の実装方法
- シグモイド関数の微分
シグモイド関数とは
シグモイド関数とは、
で表される関数です。
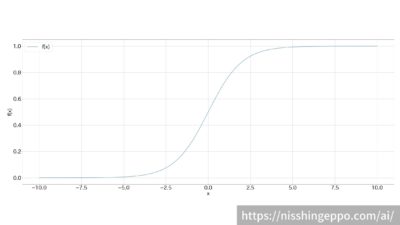
グラフで表すとこのような形になります。
シグモイド関数はディープラーニングの活性化関数の一つです。
シグモイド関数の特徴
グラフを見ると、シグモイド関数の出力は0から1の範囲に納まり、滑らかな曲線を描いています。
\(x=0\)を境に対象的なグラフとなっています。
シグモイド関数の用途
シグモイド関数は、主に2値分類問題における出力層の活性化関数に用いられます。
活性化関数にシグモイド関数を用いることで、ベルヌーイ分布を出力します。
シグモイド関数をpythonで実装
シグモイド関数をpythonで実装していきます。
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
単純な関数なので、シンプルに表すことができました。
シグモイド関数の微分
シグモイド関数の微分は高校数学の知識で行うことができます。
$$h=f(x)=\frac{1}{1+e^{-x}}$$
として微分を求めてみましょう。
\(
\frac{dh}{dx}=(-e^{-x})\left(-\frac{1}{(1+e^{-x})^2}\right)\\
\quad=\left(\frac{1}{1+e^{-x}}\right)\left(\frac{e^{-x}}{1+e^{-x}}\right)\\
\quad=\left(\frac{1}{1+e^{-x}}\right)\left(1-\frac{1}{1+e^{-x}}\right)\\
\quad=h(1-h)
\)
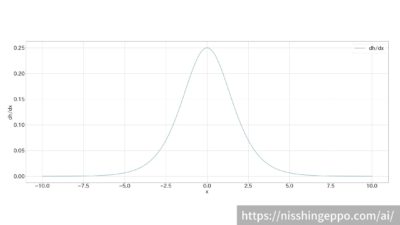
微分後の関数をグラフで表すとこのような形になります。
最大値が0.25なので勾配が小さくなっていき、勾配消失してしまいます。
まとめ
シグモイド関数とは、\(f(x)=\frac{1}{1+e^{-x}}\)で表される関数です。
0~1の範囲を滑らかにつなぐ曲線でした。
シグモイド関数は、ディープラーニングの2値分類の出力層の活性化関数としてよく使われます。
シグモイド関数の微分はシンプルに表すことができ、最大値が小さいため勾配消失が起こってしまう活性化関数です。























コメント
久保田博士の材料物理数学再武装の関数接合論も面白いよ。
初めて聞きました。
調べてみますね。