- ソフトマックス関数とは何か
- ソフトマックス関数の微分
- ソフトマックス関数の実装方法
ソフトマックス関数とは
ソフトマックス関数とは、
で表される関数です。
n個のデータがあるときに、その合計を1(100%)になるように調整してくれる関数です。
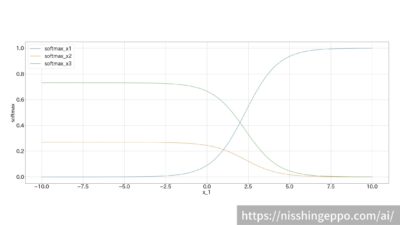
3個のデータの場合を例にグラフで表すとこのような形になります。
(x_1は変動させ、x_2=1, x_3=2に固定)
ソフトマックス関数はディープラーニングの活性化関数の一つです。
ソフトマックス関数の特徴
グラフを見ると、ソフトマックス関数では0以上1以下の値が出力されています。
それぞれの出力値を合計すると1(100%)となります。
また、データが2個の場合にはシグモイド関数になります。
ソフトマックス関数の用途
ソフトマックス関数は多クラス分類の出力層として利用されます。
出力値の合計は1(100%)となるように調整されるため、そのまま結果(確率)として使用することができます。
$$ softmax([x1, x2, x3]) = [0.2,0.3,0.5] $$
のように出力された場合、
- x1:20%
- x2:30%
- x3:50%
として結果として利用できます。
ソフトマックス関数の微分
ソフトマックス関数の微分を求めてみましょう。
$$Z = \sum _{k=1}^n e^{x_k}$$
$$h_i = f(x_i)=\frac{e^{x_i}}{\sum _{k=1}^n e^{x_k}} = \frac{e^{x_i}}{Z}$$
とします。
\( \\
i) i=jのとき\\
\frac{h_i}{dx_i} = \frac{e^{x_i}Z – e^{x_i}e^{x_i}}{Z^2} \\
\frac{h_i}{dx_i} = \frac{e^{x_i}}{Z} ( \frac{Z}{Z} – \frac{e^{x_i}}{Z} ) \\
\frac{h_i}{dx_i} = h_i(1-h_i)\\
\)
\( \\
ii) i≠jのとき\\
\frac{h_i}{dx_i} = \frac{- e^{x_i}e^{x_j}}{Z^2} \\
\frac{h_i}{dx_i} = – \frac{e^{x_i}}{Z} \frac{e^{x_j}}{Z} \\
\frac{h_i}{dx_i} = – h_i h_j \\
\)
$$\frac{h_i}{dx_j}=\begin{cases}h_i(1-h_j)\qquad (i = j)\\
-h_i h_j\qquad (i ≠j)\end{cases}$$
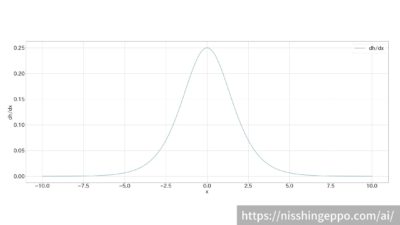
\(i=j\)のときにはシグモイド関数の微分と同様の結果となります。
\(i=j\)のときの微分後の関数をグラフで表すとこのような形になります。
ソフトマックス関数をpythonで実装
ソフトマックス関数をpythonで実装していきます。
def softmax(x):
c = np.max(x)
exp_x = np.exp(x - c)
sum_exp_x = np.sum(exp_x)
y = exp_x / sum_exp_x
return y
ソフトマックス関数を定義式のまま実装するとオーバーフローを起こしてしまう可能性があります。
指数関数(\(e^x\)が大きくならないように、任意の定数\(C\)を分母と分子に掛け算しています。
つまり、以下のような定義式を実装しています。
実装では、\(C’\)にデータの最大値を用いることでオーバーフローを防いでいます。
実装用の定義式はこのように導出できます。
\(\\
f(x_i) = \frac{e^{x_i}}{\sum _{k=1}^n e^{x_k}} \\
\qquad = \frac{C e^{x_i}}{C \sum _{k=1}^n e^{x_k}} \\
\qquad = \frac{e^{x_i + \log C}}{\sum _{k=1}^n (e^{x_k} + \log C)} \\
\qquad = \frac{e^{x_i + C’}}{\sum _{k=1}^n (e^{x_k} + C’)} \\
\)
まとめ
ソフトマックス関数とは、
$$f_i(x)=\frac{e^{x_i}}{\sum _{k=1}^n e^{x_k}}$$
で表される関数です。
ソフトマックス関数は多クラス分類の出力層として利用されます。
出力値の合計は1(100%)となるように調整されるため、そのまま結果(確率)として使用することができます。
参考文献























コメント