パーセプトロンとは?図解で分かりやすく解説!!

パーセプトロンとは

パーセプトロンとは、

 

 

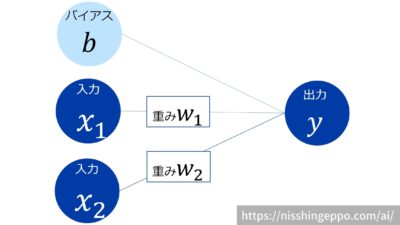
図は2つの入力を受け取るパーセプトロンです。

バイアスbと入力信号xを受け取り、それぞれに重みwが掛けられ、その総和に応じて信号yを出力します。

yへ伝わる値が0より大きいとyは1を出力し、それ以外なら0を出力します。

これを式で表すと以下のように表すことができます。

$$
y=\begin{cases}
0 & (b+w_1x_1+w_2x_2 \le 0)\\
1 & (b+w_1x_1+w_2x_2>0)
\end{cases}
$$

 

 

パーセプトロンの「○」で表されている部分は、ニューロンやノードと呼びます。

つまり、入力x、出力y、バイアスbは全てノード(ニューロン)です。

 

今回説明したパーセプトロンは、「人工ニューロン」や「単純パーセプトロン」とも呼ばれています。

 

パーセプトロンで問題を解く

パーセプトロンを使って簡単な問題を3つ問いてみます。

ANDゲート

2入力1出力のANDゲートについて考えます。

入力xが両方とも1だった場合に出力yが1になります。

 

 

ANDゲートをパーセプトロンで表現するには、条件を満たすwとbの値を見つければ良いです。

この条件を満たすwとbは無数にあり、例えば

$$
(w_1, w_2, b) = (0.5, 0.5, -0.7)
$$

のときに条件を満たします。

 

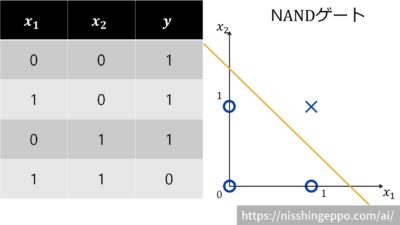
NANDゲート

2入力1出力のNANDゲートについて考えます。

入力xが両方とも1だった場合のみ出力yが0になります。

 

 

この条件を満たすwとbは無数にあり、例えば

$$
(w_1, w_2, b) = (-0.5, -0.5, 0.7)
$$

のときに条件を満たします。

 

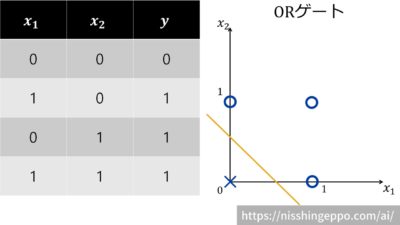
ORゲート

2入力1出力のORゲートについて考えます。

入力xのどちらか一方でも1の場合に出力yが1になります。

 

 

この条件を満たすwとbは無数にあり、例えば

$$
(w_1, w_2, b) = (0.5, 0.5, -0.3)
$$

のときに条件を満たします。

 

パーセプトロンの問題点

パーセプトロンは直線で分けることしかできないため、線形分離可能な問題しか解くことができないという問題点があります。

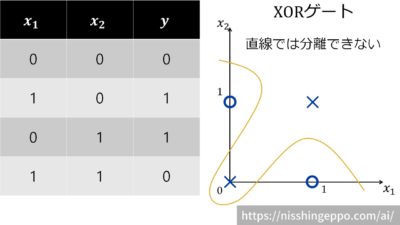
例として、2入力1出力のXORゲートを考えてみます。

 

 

XORゲートは1本の直線で分けられないため、パーセプトロンでは解決できない問題となります。

 

単純パーセプトロンでは線形の問題を表現することが限界なのですが、

パーセプトロンを重ねて使うことで非線形の表現ができるようになります。

多層パーセプトロンについてはこちらの記事にまとめてあります。

多層パーセプトロンとは?層を重ねて表現力をアップ

この記事を読んで分かること 多層パーセプトロンとは何か 多層パーセプトロンでXORゲートの表現方法 多層パーセプトロンの問題点 多層パーセプトロンのpythonでの実装方法 多層パーセプトロ...

nisshingeppo.com

 

パーセプトロンの実装(python)

パーセプトロンをpythonで実装してみました。

単純なアルゴリズムなので数行で書くことができました。

import numpy as np

def perceptron(x, w, b):
    tmp = np.sum(x*w) + b
    if tmp > 0:
        return 1
    else:
        return 0

 

作ったプログラムでANDゲートを表現して試してみましょう。

#ANDゲート
x = np.array([0, 1])
w = np.array([0.5, 0.5])
b = -0.7

print(perceptron(x, w, b))

#出力
0

xの両方の入力を1とすると、出力yが1となっていることが確認できました。

 

まとめ

パーセプトロンとは、複数の入力を受け取り、重み付けして、1つの信号を出力するアルゴリズムです。

w(重み)とb (バイアス)を調整してモデルを作成することができます。

単純パーセプトロンでは非線形の表現をすることはできません。

ただし、パーセプトロンを重ねることで表現力を増やすことができます。

 

参考文献