- 多層パーセプトロンとは何か
- 多層パーセプトロンでXORゲートの表現方法
- 多層パーセプトロンの問題点
- 多層パーセプトロンのpythonでの実装方法
多層パーセプトロンとは
多層パーセプトロンとは、
です。
単純パーセプトロンについてはこちらの記事で解説しています。

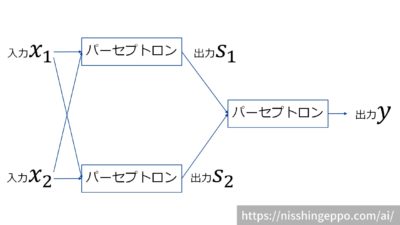
図は2入力のパーセプトロンを3つ組み合わせた2層の多層パーセプトロンです。
入力信号xを2つのパーセプトロンが受け取り、それぞれの出力を入力にしたパーセプトロンが1つあります。
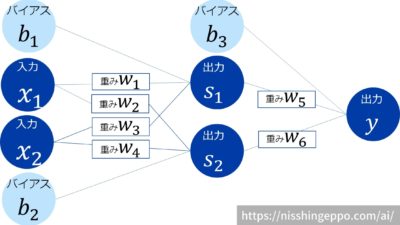
より詳細に多層パーセプトロンを図に表しました。
1つのパーセプトロンにつき重みが2つ、バイアスが1つあり、多層パーセプトロン全体のパラメータ数は9個になります。
多層パーセプトロンで問題を解く
単純パーセプトロンでは解けなかったXORゲートを多層パーセプトロンを使って表してみます。
XORゲート
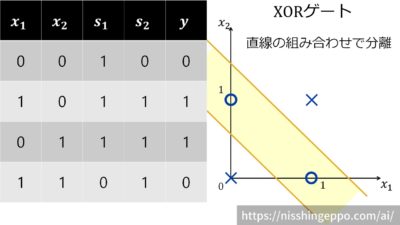
2入力1出力のXORゲートについて考えます。
入力xの値が同じ場合は出力が0になります。
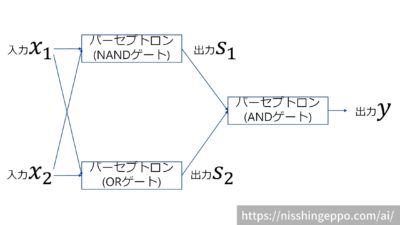
XORゲートを多層パーセプトロンで表現するには、3つのパーセプトロン(NANDゲート、ORゲート、ANDゲート)を組み合わせることで作ることができます。
入力xをNANDゲートとORゲートに入れたそれぞれの出力をsとして、そのsをANDゲートの入力にすることで、XORゲートを表現しています。
非線形の問題であるXORゲートも線形モデルの組み合わせで解くことができました。
多層パーセプトロンの問題点
多層パーセプトロンで非線形な問題を解けるようになったのですが、何でもできるわけではありません。
多層パーセプトロンには問題点があります。
ということです。
XORゲートを表現するときにも、各パーセプトロンの重みは真理値表を見ながら手動で決定しました。
この問題を解消した手法が、ニューラルネットワークとなります。
多層パーセプトロンの実装(python)
多層パーセプトロン(XORゲート)をpythonで実装してみました。
単純パーセプトロンの組み合わせで表現することができます。
まずは、パーセプトロンを作成します。
import numpy as np
def perceptron(x, w, b):
tmp = np.sum(x*w) + b
if tmp > 0:
return 1
else:
return 0
パーセプトロン(ANDゲート、ORゲート、NANDゲート)を使ってXORゲートを表現して試してみました。
def xor_gate(x):
#NAND
w = np.array([-0.5, -0.5])
b = 0.7
s1 = perceptron(x, w, b)
#OR
w = np.array([0.5, 0.5])
b = -0.2
s2 = perceptron(x, w, b)
#AND
w = np.array([0.5, 0.5])
b = -0.7
s = np.array([s1, s2])
y = perceptron(s, w, b)
return y信号を入力して正しい出力が出ることを確認します。
x = np.array([[0, 0],[0, 1],[1, 0],[1, 1]])
for i in x:
print("入力:" + str(i) + " 出力:" + str(xor_gate(i)))#出力 入力:[0 0] 出力:0 入力:[0 1] 出力:1 入力:[1 0] 出力:1 入力:[1 1] 出力:0
xの値が同じ場合には0が出力されることが確認できました。
まとめ
多層パーセプトロンとは、単純パーセプトロンを複数重ね合わせたものです。
単純パーセプトロンでは線形なものしか表現できませんでしたが、多層パーセプトロンでは非線形なものも表現できるようになりました。
XORゲートの問題を多層パーセプトロンで解き、pythonで実装も行いました。






















コメント