勾配降下法とは?分かりやすく図解で解説

この記事を読んで分かること

勾配降下法とは?

勾配降下法とは、

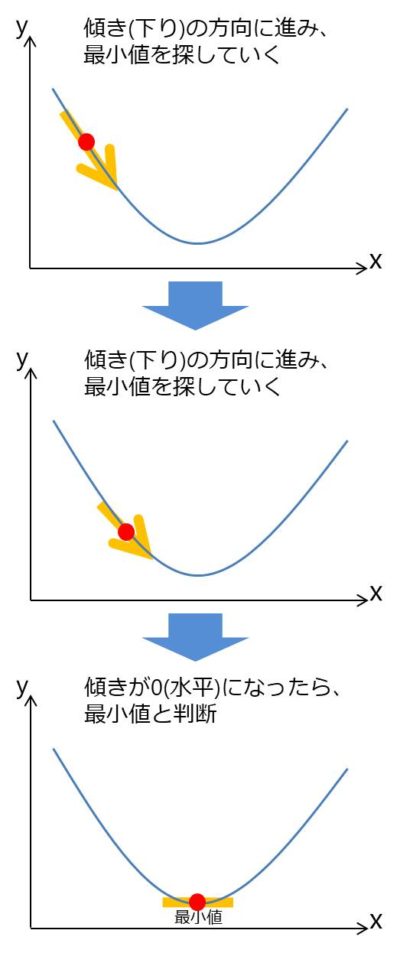
関数の傾きを元に最小値を探す手法

です。

下の図のように、今いる点のグラフの傾きを見て、下っている方向を探索する手法になります。

グラフを見ればどこが最小値かなんてひと目で分かると思ってしまいますが、データの量が多いと全体を把握できません。

一部のデータだけで最小値を見つけるように考えられた方法となります。

例えば、ディープラーニングでは、誤差が最小値となる重み(パラメータ)を探すために使われています。

勾配降下法は、利用するデータの量によって3種類に分けられます。

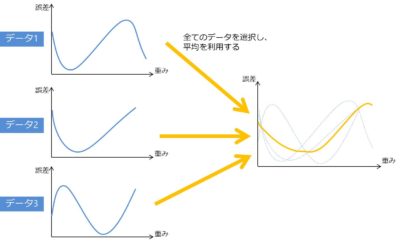
バッチ勾配降下法では、全データを使って関数の最小値を探索します。

つまり全てのデータの平均のデータに対して勾配降下法を使うイメージになります。

そのため、すべてのデータの勾配を計算して覚えておく必要があるので、計算時間もメモリの消費も大きくなる手法です。

メリットは以下のことが考えられます。

デメリットとしては以下のことが考えられます。

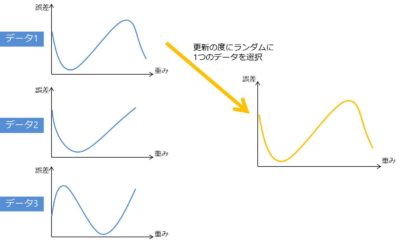
SGD(確率的勾配降下法)では、ランダムに抽出した1つのデータを使って関数の最小値を探索します。

メリットは以下のことが考えられます。

デメリットとしては以下のことが考えられます。

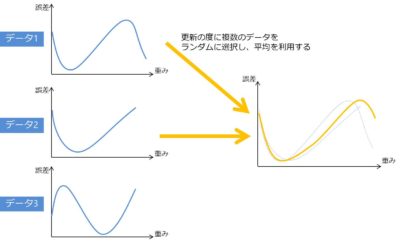
ミニバッチ勾配降下法は、SGDとバッチ勾配降下法の間をとった方法になります。

データの一部を利用して、関数の最小値を探索します。

特徴としては、SGDとバッチ勾配降下法のハイブリッドであるので、それぞれの良い点と悪い点の両方を持っています。

そのため、バランスの良い手法と言えます。

手法	利用データ	計算時間	メリット	デメリット
バッチ勾配降下法 (最急降下法)	全てのデータを利用	大	・解への到達が早いことが多い・結果が安定する	・メモリの使用量が多い・局所解にハマりやすい
SGD (確率的勾配降下法)	1つのデータを利用	小	・メモリの使用量が少ない・オンライン学習が可能・局所解を回避できる可能性がある	・解への到達が遅いことがある・外れ値の影響を大きく受ける
ミニバッチ勾配降下法	一部のデータを利用	中	バッチ勾配降下法とSGDのそれぞれのメリットがある。	バッチ勾配降下法とSGDのそれぞれのデメリットがある。