サポートベクターマシン(SVM)とは?マージン最大化で推測する手法!!

サポートベクターマシン(SVM)とは?

サポートベクターマシン(SVM)は、マージン最大化という基準を用いて決定境界を得るモデルです。

サポートベクターマシンは分類と回帰のどちらの問題にも利用することもできます。

このアルゴリズムでは、決定境界は線形になります。

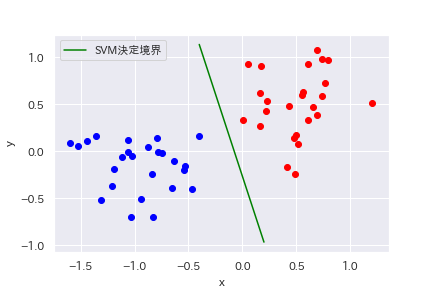
縦軸、横軸に特徴量をとったグラフにプロットされたデータが決定境界(直線)で分類されています。

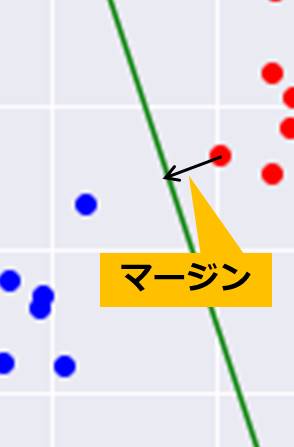
決定境界から一番近いデータまでの距離をマージンと呼び、マージンが最大になるように決定境界の位置が決められています。

ロボくん

サポートベクターマシンは、境界から一番近いデータの距離を最大にするように分類する方法だね。

サポートベクターマシンの決定境界の決め方

サポートベクターマシンの決定境界の決め方には「ソフトマージン」と「ハードマージン」の2種類があります。

ハードマージンは、直線できれいに分離することができるデータに対して利用することができます。

ハードマージンでは、1つでも外れ値があるとそのデータの影響を大きく受けてしまいます。

Cの値が小さい場合には、決定境界の内側にあるデータ数は増え、Cの値が限りなく大きい場合には、ハードマージンとなります。

ロボくん

完璧を求め過ぎないソフトマージンを利用することで、学習結果の外れ値がある場合でも推定することができるんだね。

サポートベクターマシン(SVN)をpythonで実装

サポートベクトルマシンの計算例をpythonで実装してみました。

今機械学習のライブラリであるsklearnを使いソフトマージンで分類を行います。

必要ライブラリのインポート

import matplotlib.pyplot as plt
import numpy as np

from sklearn.svm import LinearSVC
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

データの生成

#データ生成
centers = [(-1, -0.125), (0.5, 0.5)]
X, y =make_blobs(n_samples=50, n_features=2, centers=centers, cluster_std=0.3)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

#データの色分け
X_blue = X[y==0,:]
X_red = X[y==1,:]

サポートベクターマシンのモデルで学習する

#サポートベクターマシンで分類する
model = LinearSVC()
model.fit(X_train, y_train)#学習
y_pred = model.predict(X_test)#推定
accuracy_score(y_pred, y_test)#正解率

ちなみに、今回のテストデータでは単純なため、正解率は100%となりました。

結果の表示

#結果の描画
plt.scatter(X_blue[:,0],X_blue[:,1],c="blue")
plt.scatter(X_red[:,0],X_red[:,1],c="red")
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c="green",label="SVM決定境界")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()

決定境界によって、データが綺麗に分類されていることが分かります。

まとめ

サポートベクターマシンとは何かをまとめると以下の3つの特徴を持つモデルです。