- loglossとは何か
loglossとは
loglossとは、
です。
機械学習において、loglossは交差エントロピー(クロスエントロピー)と同じものとなります。
変数の意味は以下の通りです。
\(y_i\log{p_i}\)の部分が正例のときの誤差を表し、
\((1-y_i)\log{(1-p_i)}\)の部分が負例のときの誤差を表しています。
loglossは低いほど誤差が少なく、良い指標です。
定義式だけではよくわからないと思うので、具体例を見ていきましょう。
loglossの具体例
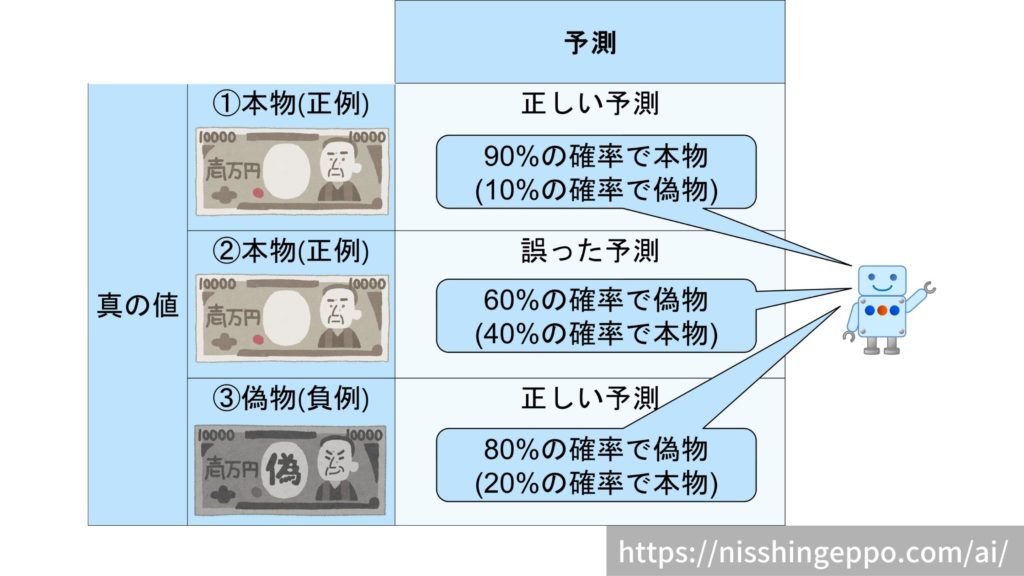
3枚のお札をAIが判定した結果を例として考えてみます。
| ID | y (正例が1、負例が0) | p (正例の確信度) |
| 1 | 1 | 0.9 |
| 2 | 1 | 0.4 |
| 3 | 0 | 0.2 |
まずは、IDごとに誤差を求めていきましょう。
$$(ID:1の誤差)=- 1\log{0.9}+(1-1)\log{(1-0.9)} = -\log{0.9}$$
$$(ID:2の誤差)=- 1\log{0.4}+(1-1)\log{(1-0.4)} = -\log{0.4}$$
$$(ID:3の誤差)=- 0\log{0.2}+(1-0)\log{(1-0.2)} = -\log{0.8}$$
これらの誤差の平均値がloglossとなります。
$$logloss=- \frac{1}{3} (\log{0.9}+\log{0.4}+\log{0.8})=0.41$$
loglossでは、正例の確率を高く予測したものが間違っているとペナルティが大きく与えられるようになっています。
逆の間違い(負例の確率を高く予測したものが間違っている場合)も同様に大きなペナルティが与えられます。
pythonでloglossを求める
loglossはscikit-learnライブラリで計算することができます。
from sklearn.metrics import log_loss
y = [1, 1, 0]
p = [0.9,0.4,0.2]
logloss = log_loss(y, p)
print(logloss)
#0.414931599615397
まとめ
loglossとは、
$$logloss=- \frac{1}{N} \sum ^{n}_{i=1}y_i\log{p_i}+(1-y_i)\log{(1-p_i)}$$
で表される分類型タスクの評価指標です。
機械学習において、loglossは交差エントロピー(クロスエントロピー)と同じものとなります。
pythonではscikit-learnライブラリを使うことでloglossを容易に計算することができます。






















コメント