- 混同行列とは何か
- 真陽性・偽陰性・偽陽性・真陰性の違い
- 混同行列を使った評価指標にはどんなものがあるのか
混同行列とは
混同行列とは、
です。
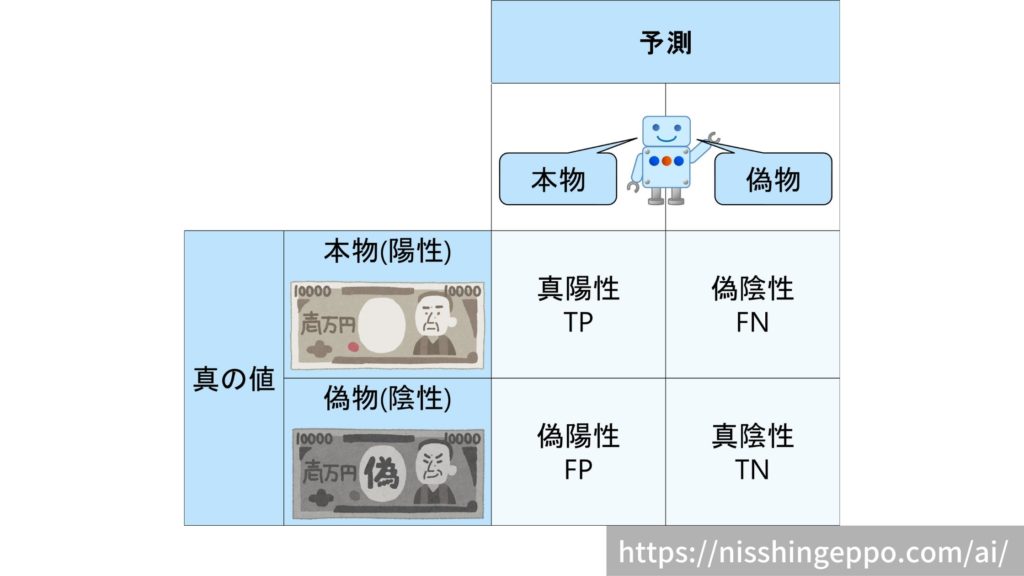
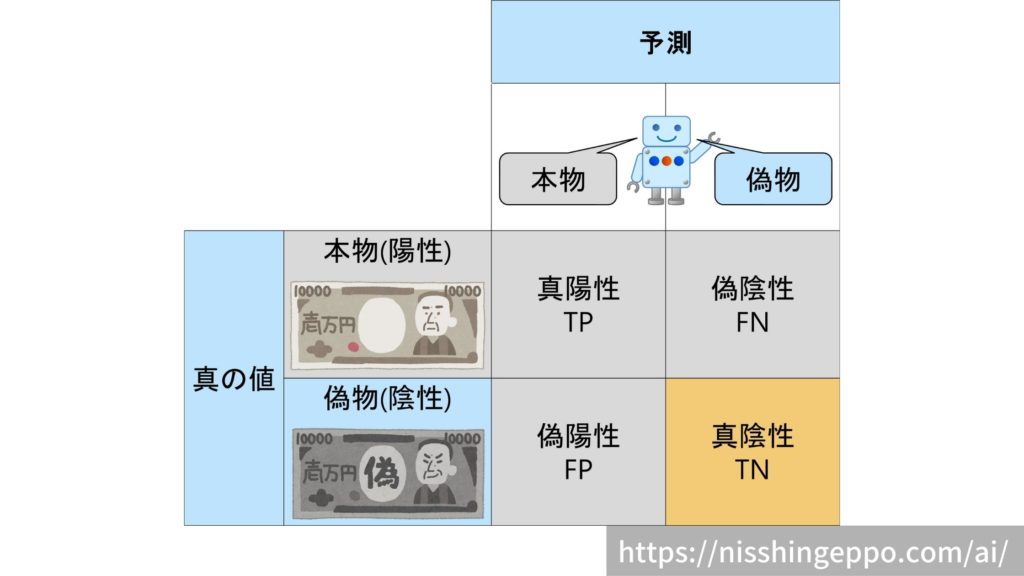
具体的な混同行列は以下のようなイメージとなります。
マトリクスからも分かるように、2値分類の結果(正解・不正解)には4種類あります。
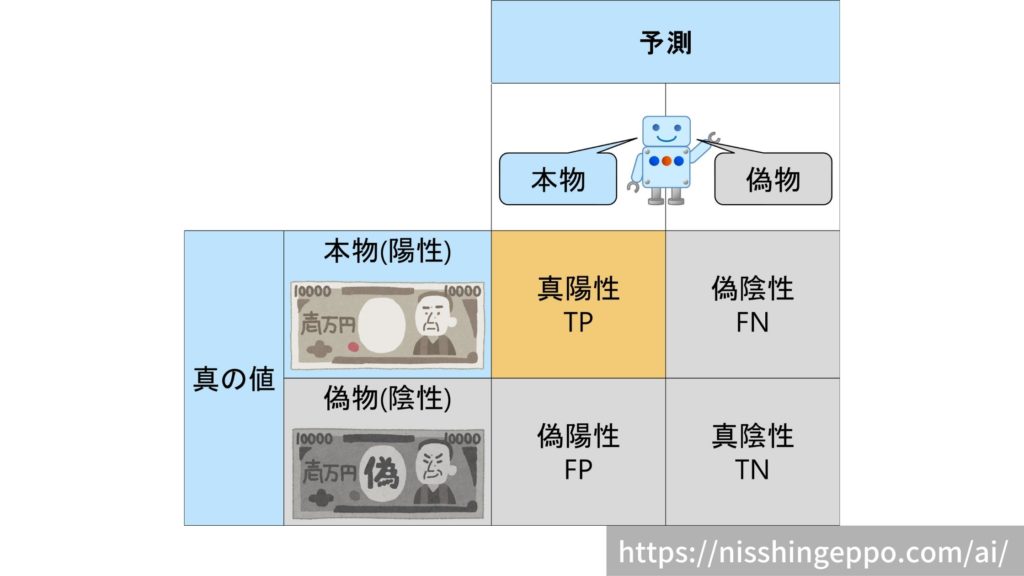
真陽性(True Positive)
本物(陽性)であるものを本物(陽性)だと予測するパターンです。
真の値と予測が一致しているので正解となります。
正解なので、真陽性の割合は高い方が望ましいです。
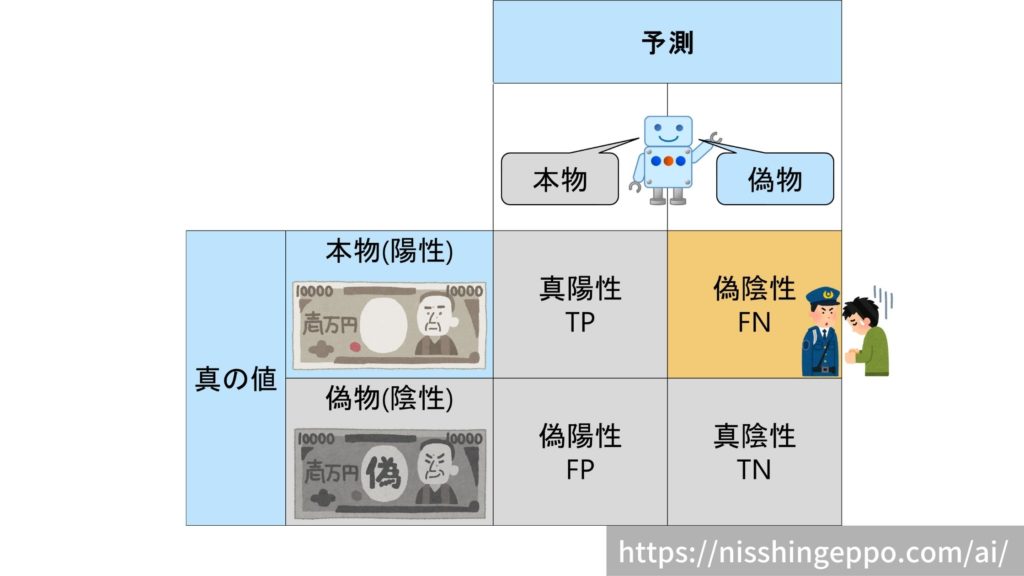
偽陰性(False Negative)
本物(陽性)であるものを偽物(陰性)だと予測するパターンです。
本物の判別を誤るため、冤罪としてしまいます。
真の値と予測が一致していないので不正解となります。
不正解なので、偽陽性の割合は低い方が望ましいです。
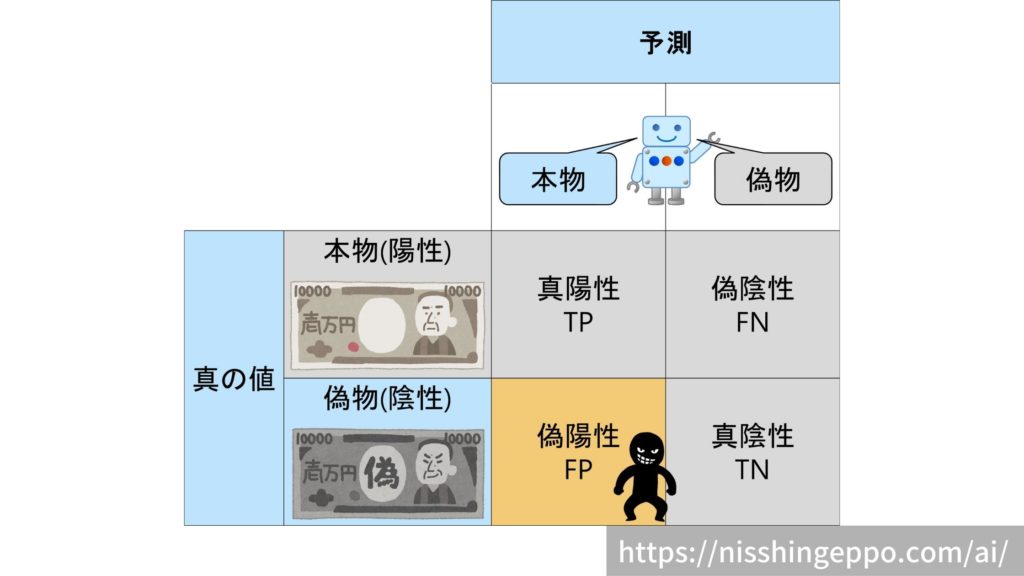
偽陽性(False Positive)
偽物(陰性)であるものを本物(陽性)だと予測するパターンです。
偽物を見逃しているため、犯罪者が喜ぶ誤り方です。
真の値と予測が一致していないので不正解となります。
不正解なので、偽陰性の割合は低い方が望ましいです。
真陰性(True Negative)
偽物(陰性)であるものを偽物(陰性)だと予測するパターンです。
真の値と予測が一致しているので正解となります。
正解なので、真陰性の割合は高い方が望ましいです。
混合行列を使った評価指標
混合行列を使い2値分類の結果(正解・不正解)を整理することができました。
次は、予測モデルの精度を評価していきましょう。
混合行列を用いた評価指標を7個の一覧です。
| 評価指標 | 計算式 |
| 正解率(accuracy) | $$\frac{TP+TN}{TP+TN+FP+FN} $$ |
| 誤答率(error rate) | $$1-accuracy $$ |
| 適合率(precision) | $$\frac{TP}{TP+FP} $$ |
| 再現率(recall) | $$\frac{TP}{TP+FN} $$ |
| F値(F1-score) | $$\frac{2}{\frac{1}{recall}+\frac{1}{precision}} $$ |
| F値(Fβ-score) | $$\frac{1+β^2}{\frac{β^2}{recall}+\frac{1}{precision}} $$ |
| MCC (Matthews Correlation Coefficient) | $$\frac{TP×TN-FP×FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}} $$ |
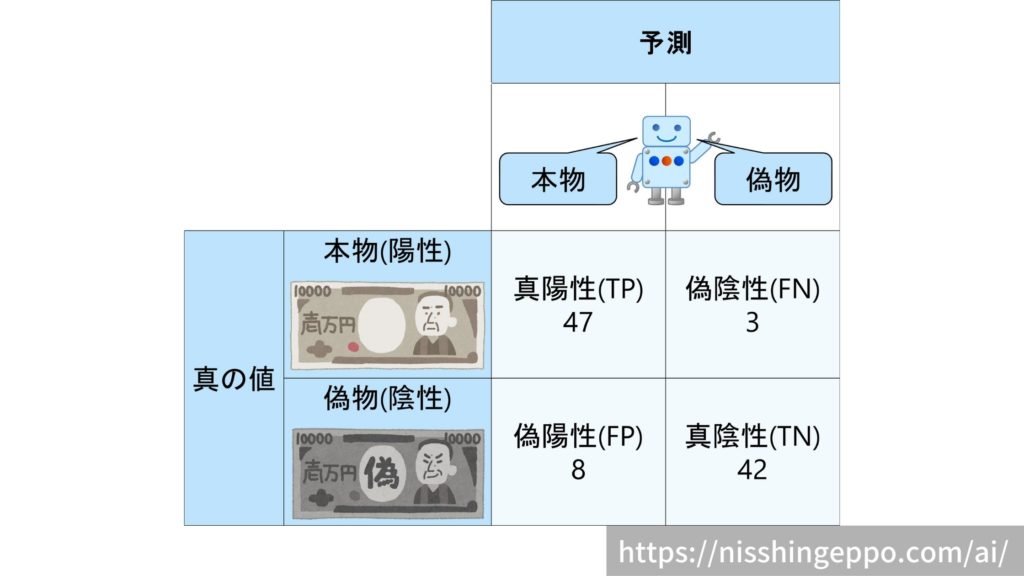
こちらの全100データの混合行列を例として、各評価指標の説明していきたいと思います。
正解率(accuracy)
正解率(accuracy)は予測が正しい割合(全体の何%が正解したのか)を表す指標です。
$$accuracy = \frac{正解したデータ}{全データ}=\frac{TP+TN}{TP+TN+FP+FN} $$
直感的に理解しやすい評価指標となっています。
具体例で計算をしてみると、
$$accuracy = \frac{47+42}{47+42+3+8}=0.89 $$
といった結果となりました。
こちらの記事でもっと詳しく解説しています。

誤答率(error rate)
誤答率(error rate)は予測が誤った割合(全体の何%が不正解したのか)を表す指標です。
$$error rate = 1-accuracy$$
直感的に理解しやすい評価指標となっています。
具体例で計算をしてみると、
$$error rate= 1-0.89=0.11 $$
といった結果となりました。
誤答率(error rate)も不均衡なデータ(陽性が90%など)の場合、正しく評価し辛い指標となっています。
適合率(precision)
適合率(precision)は本物(陽性)と予測したもののうち何%が正解したのかを表す指標です。
$$precision= \frac{正解したデータ}{本物と予測したデータ}=\frac{TP}{TP+FP} $$
誤検知を少なくしたい場合は適合率(precision)を重要視します。
具体例で計算をしてみると、
$$precision= \frac{47}{47+8}=0.85 $$
といった結果となりました。
適合率(precision)は次に紹介する再現率(recall)とトレードオフの関係となっています。
適合率についてはこちらの記事でもっと詳しく解説しています。

再現率(recall)
再現率(recall)は本物(陽性)のデータのうち何%正解できたかを表す指標です。
$$recall= \frac{正解したデータ}{本物のデータ}=\frac{TP}{TP+FN} $$
本物(陽性)の見逃しを避けたい場合は適合率(precision)を重要視します。
具体例で計算をしてみると、
$$precision= \frac{47}{47+3}=0.94 $$
といった結果となりました。
再現率(recall)は適合率(precision)とトレードオフの関係となっています。
再現率についてはこちらの記事でもっと詳しく解説しています。

F値(F1-score)
F1-scoreは前述の適合率(precision)と再現率(recall)の調和平均で計算される指標です。
$$F1score= \frac{2}{\frac{1}{recall}+\frac{1}{precision}} $$
適合率(precision)と再現率(recall)のバランスを取った指標のため、実務でもよく使用されます。
具体例で計算をしてみると、
$$F1score= \frac{2}{\frac{1}{0.94}+\frac{1}{0.854}} = 0.895$$
といった結果となりました。
F値についてはこちらの記事でもっと詳しく解説しています。

F値(Fβ-score)
Fβ-scoreは前述のF1-scoreで、適合率(precision)と再現率(recall)のバランスを調整できるようにした指標です。
$$Fβscore= \frac{1+β^2}{\frac{β^2}{recall}+\frac{1}{precision}} $$
βを大きくするほど再現率(recall)が重視された指標になります。
β=0.1として具体例で計算をしてみると、
$$Fβscore= \frac{1+0.1^2}{\frac{0.1^2}{0.94}+\frac{1}{0.854}} = 0.855$$
といった結果となりました。
MCC(Matthews Correlation Coefficient)
MCC(Matthews Correlation Coefficient)は不均衡なデータに対して性能を評価しやすい指標です。
$$MCC= \frac{TP×TN-FP×FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}$$
MCCはあまり使われる頻度は高くありません。
具体例で計算をしてみると、
$$MCC= \frac{47×42-8×3}{ \sqrt{(47+8)(47+3)(42+8)(42+3)} } = 0.784$$
といった結果となりました。
MCCについてはこちらの記事でもっと詳しく解説しています。

まとめ
混同行列とは、2値分類の結果(正解・不正解)をとりまとめるために使われるマトリクス(行列)です。
分類問題の結果には以下の4種類があります。
- 真陽性(True Positive)
- 偽陰性(False Negative)
- 偽陽性(False Positive)
- 真陰性(True Negative)
混合行列を使って4種類の結果を整理し、評価指標を計算することができます。






















コメント
偽陰性と偽陽性のたとえの部分逆ではないでしょうか。
分かり辛い例えをしてしまいましたが、表としては正しい情報化と思います。
本物だと判断するのが陽性、偽札だと判断するのが陰性ですので、陰性が悪い人としています。
臨床検査では陽性が罹患(悪い)とするので紛らわしい例ですね。
コメントありがとうございます。