- 正解率(Accuracy)とは何か
- 正解率(Accuracy)の具体的な計算方法
正解率(Accuracy)とは
正解率(Accuracy)とは、
です。
$$accuracy = \frac{正解したデータ}{全データ}$$で表されます。
正しく予測できたものは混合行列でいうと真陽性(本物を本物と予測したもの)と真陰性(偽物を偽物と予測したもの)です。
つまり正解率(Accuracy)は以下の式で表すことができます。
$$accuracy = \frac{正解したデータ}{全データ}=\frac{TP+TN}{TP+TN+FP+FN} $$

混合行列が分からない場合はこちらの記事で解説しているので、読んでみてください。

正解率(Accuracy)を実際に計算してみる
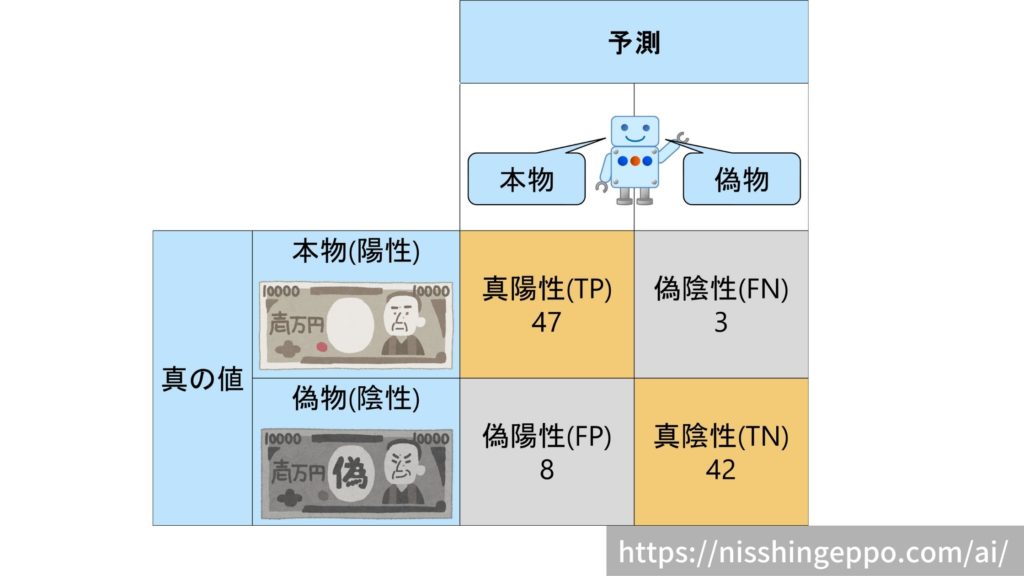
本物のお札50枚と偽物のお札50枚の計100枚のお札を判定する例を考えてみます。
本物(TP)と正しく判断できたものが47枚、偽物(TN)と正しく判断できたものが42枚です。
これらの合計の89枚が正解できたものとなります。
そのため、
$$accuracy = \frac{TP+TN}{TP+TN+FP+FN} = \frac{47+42}{47+42+8+3}=0.89 $$
となり、正解率(Accuracy)は0.89(89%)です。
データが偏っていると正しく評価しづらい
正解率(accuracy)は不均衡なデータ(陽性が90%など)の場合、正しく評価し辛くなります。
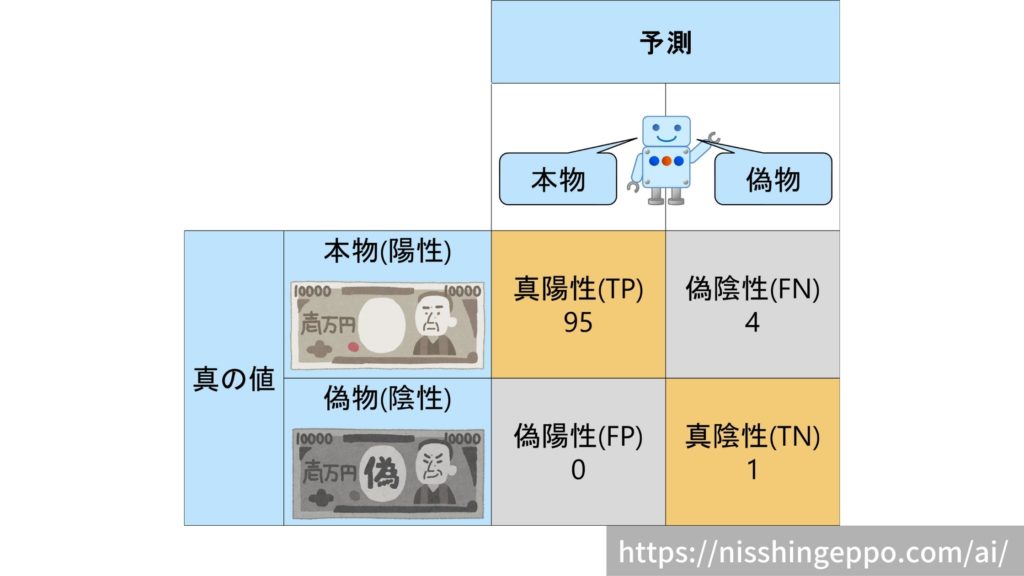
例えば、本物が99枚、偽物が1枚の計100枚のお札をAIで分類したときの例を考えてみましょう。
このときの正解率は、
$$accuracy = \frac{TP+TN}{TP+TN+FP+FN} = \frac{95+1}{95+1+0+4}=0.96 $$
となり、正解率(Accuracy)は0.96(96%)です。
一見きちんと評価できているように見えます。
ここで、どんなデータであっても本物と判断するAIについても正解率を計算してみましょう。
$$accuracy = \frac{TP+TN}{TP+TN+FP+FN} = \frac{99+0}{99+0+1+0}=0.99 $$
となり、正解率(Accuracy)は0.99(99%)です。
何も考えずに本物と判断するAI(偽札を一切見抜けないAI)の方が優れているという結果になってしまいました。
このように偏ったデータから算出した正解率だけでAIの良し悪しを検討すると、目的に合わない判断をしてしまうことがあります。
まとめ
正解率(Accuracy)とは、混同行列を使った評価指標の1つで、AIが正しく予測できた割合(全体の何%が正解したのか)を表す評価指標です。
$$accuracy = \frac{正解したデータ}{全データ}$$で表されます。
正解率(accuracy)は不均衡なデータ(陽性が90%など)の場合、正しく評価し辛くなります。






















コメント