- 適合率(precision)とは何か
- 適合率(precision)の具体的な計算方法
適合率(precision)とは
適合率(precision)とは、
です。
$$precision = \frac{本物のデータ}{本物だと予測したデータ}$$で表されます。
本物のデータは混合行列でいうと真陽性(本物を本物と予測したもの)です。
本物だと予測したものは混合行列でいうと偽陽性(偽物を本物と予測したもの)と偽陰性(本物を偽物と予測したもの)です。
つまり適合率(precision)は以下の式で表すことができます。
$$precision = \frac{本物のデータ}{本物だと予測したデータ}=\frac{TP}{TP+FP} $$

混合行列が分からない場合はこちらの記事で解説しているので、読んでみてください。

適合率(precision)を実際に計算してみる
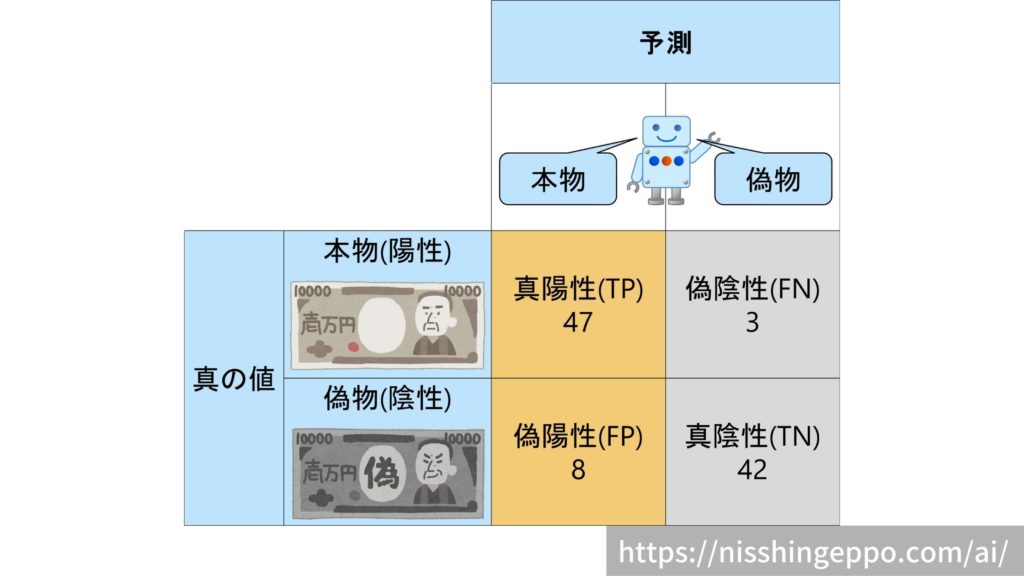
本物のお札50枚と偽物のお札50枚の計100枚のお札を判定する例を考えてみます。
本物を正しく判断した(TP)が47枚です。
本物だと予測したもの(TP+FP)が55枚です。
そのため、
$$precision = \frac{TP}{TP+FP} = \frac{47}{47+8}=0.86 $$
となり、適合率(precision)は0.86(86%)です。
適合率(precision)は再現率(recall)とトレードオフ
適合率(precision)は再現率(recall)とトレードオフの関係になっています。
つまり、どちらかの値を高くしようとすると、もう一方の値は低くなります。
逆に、片方の指標を無視すればもう一つの指標は1に近づけることができます。
再現率(recall)についてはこちらの記事で説明しています。

適合率を高くする例
自信のないものは偽物と判断するようにAIを設定すれば、適合率(precision)は高くなります。
$$precision = \frac{TP}{TP+FP} = \frac{9}{9+1}=0.9 $$
となり、適合率(precision)は0.9(90%)です。
適合率を高くする例
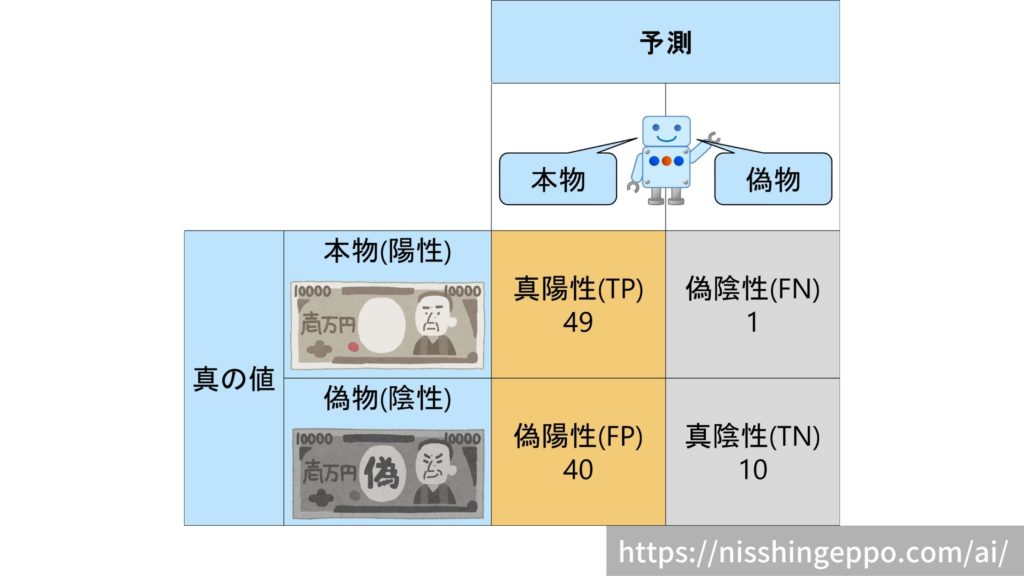
また、本当に本物か怪しいものまで本物と判断するようにAIを設定すれば、適合率(precision)は低くなります。
$$precision = \frac{TP}{TP+FP} = \frac{49}{49+40}=0.55 $$
となり、適合率(precision)は0.55(55%)です。
AIのモデルを評価するときは、適合率(precision)だけの値で評価せず、再現率(recall)とのバランスを考慮したF値などがよく使われます。
まとめ
適合率(precision)とは、混同行列を使った評価指標の1つで、AIが正例だと予測をしたものの内、正解した割合を表す評価指標です。
$$precision = \frac{本物のデータ}{本物だと予測したデータ}=\frac{TP}{TP+FP} $$で表されます。
適合率(precision)は再現率(recall)とトレードオフの関係になっています。























コメント