- AUCとは何か
- ROC曲線の書き方
AUC(Area Under the ROC Curve)とは
AUCとは、
です。
縦軸を真陽性率(全体の内、正しく正例と予測した正例の割合)、
横軸を偽陽性率(全体の内、誤って正例と予測した負例の割合)
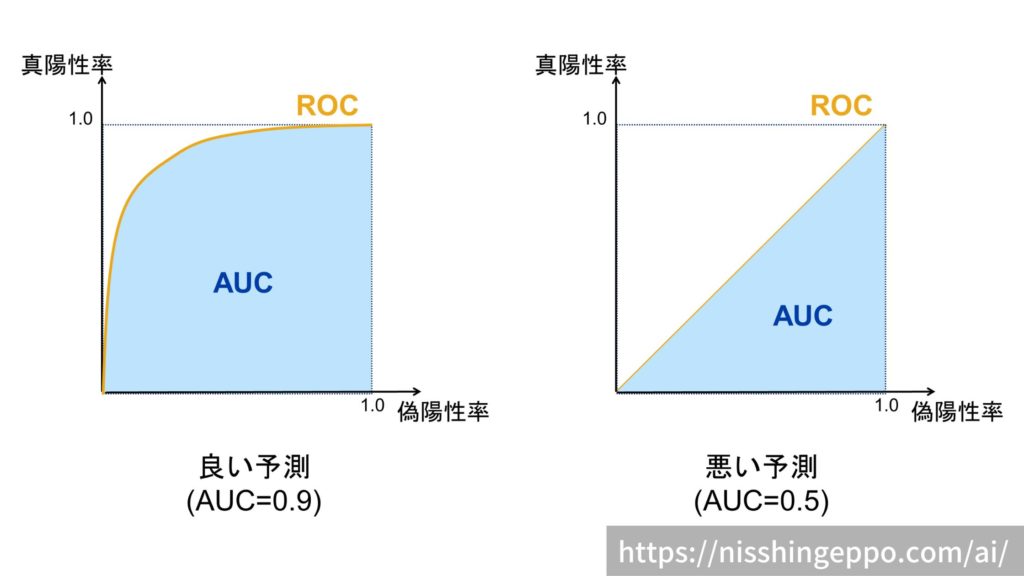
をとって以下のように図示できます。
予測精度の良いときにはAUCは1に近づき、予測精度の悪い(ランダムな予測)ときには0.5になります。
真陽性と偽陽性についてわからない場合はこちらの記事で解説をしているので読んでみて下さい。

AUCの特徴として、正例が少ない不均衡データの場合、正例の確信度をどれだけ高められるかがAUCに大きく影響します。
逆に、負例の予測値の誤差はあまり影響を与えません。
ROC曲線の書き方
ROC曲線は、閾値をずらしたときの真陽性率と偽陽性率の関係をプロットしたものです。
言葉だけでは分かりづらいので、具体例で考えてみましょう。
今回は、9枚のお札(本物5枚、偽物4枚)をAIで予測した結果を使っていきます。
まず、100%を閾値とすると、本物であると分類されるものは0枚となります。
$$真陽性率= \frac{真陽性}{正データ}=\frac{0}{5} =0$$
$$偽陽性率= \frac{偽陽性}{偽データ}=\frac{0}{4} =0$$
この真陽性率と偽陽性率をプロットします。
次に90%を閾値とすると、本物であると分類されるものは2枚(2,4枚目)となります。
$$真陽性率= \frac{真陽性}{正データ}=\frac{2}{5} =0.4$$
$$偽陽性率= \frac{偽陽性}{偽データ}=\frac{0}{4} =0$$
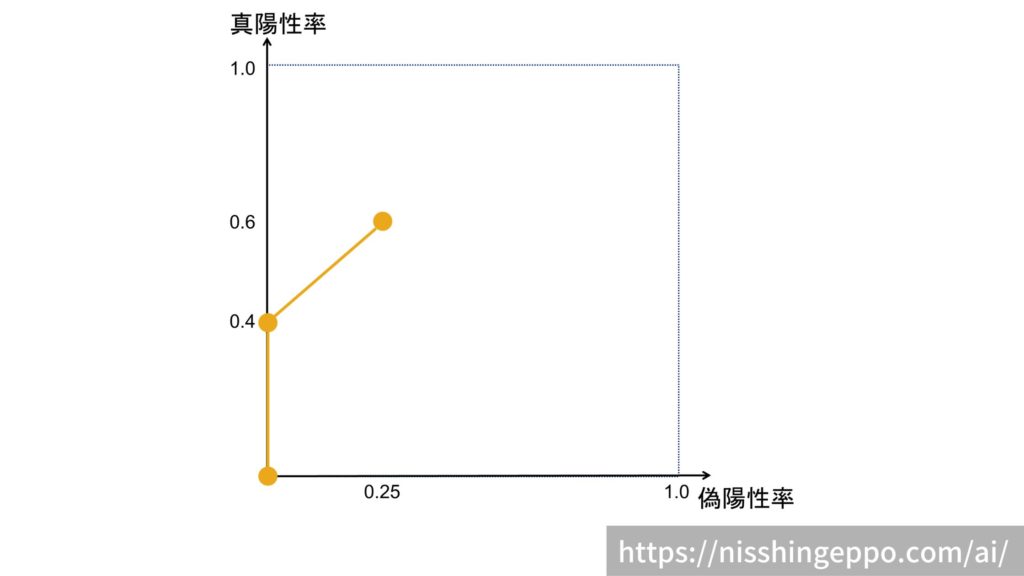
80%を閾値とすると、本物であると分類されるものは4枚(1,2,4,8枚目)となります。
$$真陽性率= \frac{真陽性}{正データ}=\frac{3}{5} =0.6$$
$$偽陽性率= \frac{偽陽性}{偽データ}=\frac{1}{4} =0.25$$
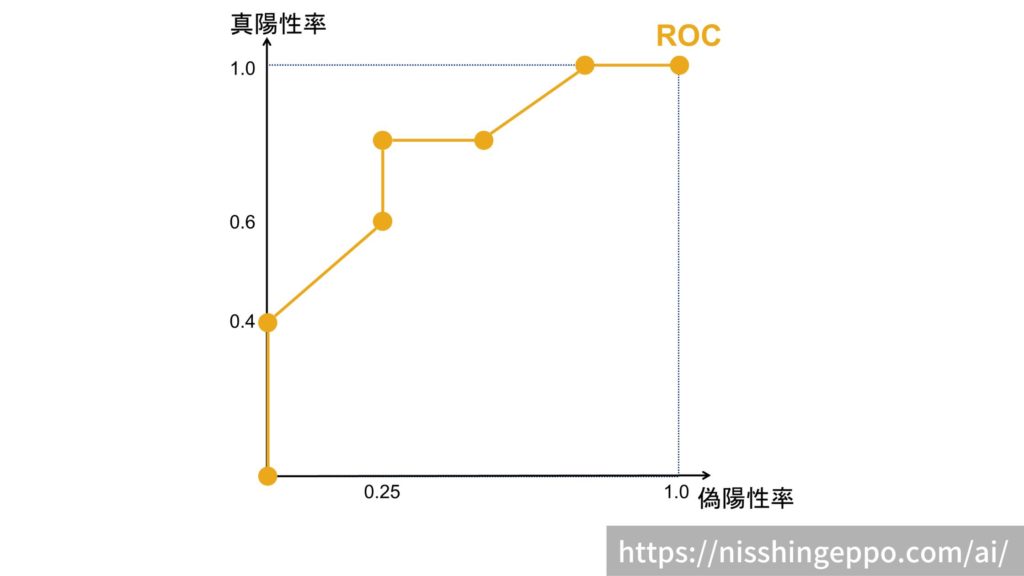
このように閾値をずらしていき、真陽性率と偽陽性率の関係をプロットしていくと最終的にROC曲線を描くことができます。
まとめ
AUCとは、2値分類における代表的な評価指標の1つで、ROC曲線の下部の面積のことです。
真陽性率と偽陽性率から求めることができ、予測精度の良いときにはAUCは1に近づき、予測精度の悪い(ランダムな予測)ときには0.5となる特徴があります。
ROC曲線は、閾値をずらしたときの真陽性率と偽陽性率の関係をプロットしていくと描くことができあます。

























コメント