線形回帰(Linear Regression)は、教師あり学習の一つの手法です。
回帰問題の予測を行うシンプルなアルゴリズムとなっています。
線形回帰(Linear Regression)とは?
線形回帰とは、「目的変数(予想したい値)が説明変数(関係する値)の関数で表せる」という仮説を立てモデル化する手法です。
つまり、
$$y=f(x)$$
で表せることを仮定して分析するということです。
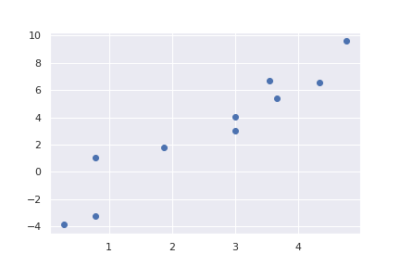
データ(xとy)に相関関係が見られるようなデータを
関数化して近似するモデルとなります。

バラバラになっているデータから特徴を掴んで、関数のグラフに近似するのが線形回帰だね!!
線形回帰の種類
線形回帰は、説明変数が1つでない場合や1次式以外の関数へのモデル化も行うことができます。
「線形」回帰とは一体何なのかと疑問に思うかもしれませんが、変数の係数(a)が1次しか取らないので線形回帰と呼ばれています。
| 線形回帰の種類 | 線形回帰の数式 |
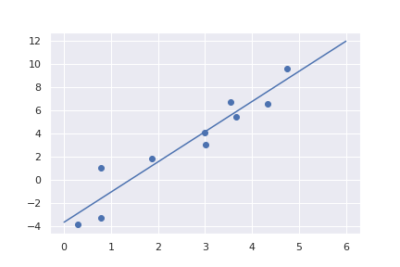
| 単回帰 | $$y=ax + b$$ |
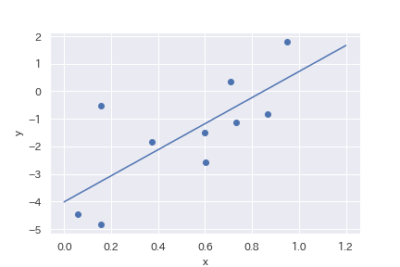
| 重回帰 | $$y=a_0x + a_1x + … + b$$ |
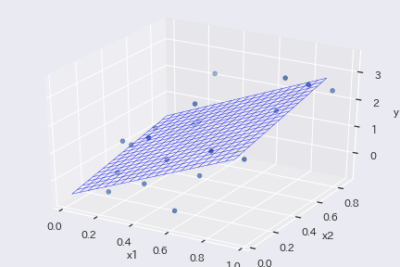
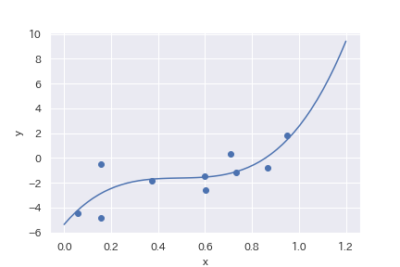
| 多項式回帰 | $$y=a_0x + a_1x^2 + … + b$$ |
重回帰(変数x1,x2)
多項式回帰(xの3次関数)

線形回帰といっても直線以外に適用もできるんだね!!




















コメント