- どのような活性化関数があるか
活性化関数は、ディープラーニングの学習において重要な役割を担っています。
学習モデルを作る際に利用するパラメータの1つでもあり、様々な関数があるのでどんなものがあるか知っておきましょう。
活性化関数一覧
早速、主な活性化関数の一覧をまとめました。
| 線形回帰の種類 | 線形回帰の数式 |
| elu | $$ f(x)=\begin{cases} x & (0 \le x)\\ α(e^{x}-1) & (x<0) \end{cases} $$ |
| selu | $$ f(x)=\begin{cases} λx & (0 \le x)\\ λα(e^{x}-1) & (x<0) \end{cases} $$ |
| softsign | $$f(x)=\frac{x}{1+|x|}$$ |
| relu | $$ f(x)=max(0,x)= \begin{cases} x & (0 \le x) \\ -x & (x < 0) \end{cases} $$ |
| tanh | $$f(x)=tanh(x)=\frac{e^{-x}-e^{x}}{e^{-x}+e^{x}}$$ |
| sigmoid | $$f(x)=\frac{1}{1+e^{-x}}$$ |
| hard_sigmoid | $$f(x)=\begin{cases}1 & (2.5 < x) \\0.2x+0.5(e^{x}-1) & (-2.5 \le x \le 2.5)\\0 & (x < -2.5)\end{cases}$$ |
| linear | $$f(x)=x$$ |
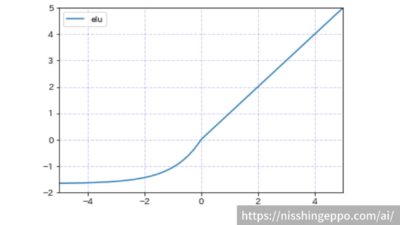
elu(Exponential Liner Units)
eluは入力が0以上の場合には出力はそのままで、入力が0以下では-αに収束するような関数です。
大きな負の入力については、ほとんど違いが出ないようになっています。
$$f(x)=\begin{cases}
x & (0 \le x)\\
α(e^{x}-1) & (x<0)
\end{cases}
$$
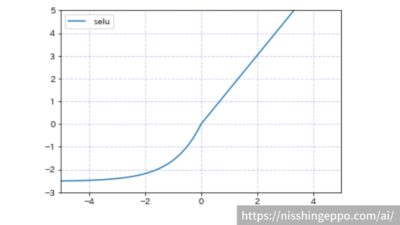
selu(Scaled Exponential Liner Units)
seluは入力が0以上の場合にはλ倍し、入力が0以下では-λαに収束するような関数です。
正の入力の変化には敏感になり、大きな負の入力については、ほとんど違いが出ないようになっています。
$$
f(x)=\begin{cases}
λx & (0 \le x)\\
λα(e^{x}-1) & (x<0)
\end{cases}
$$
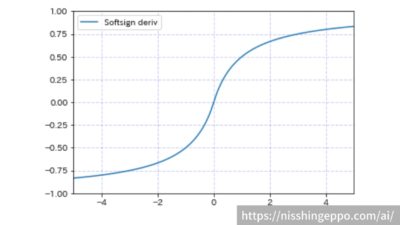
softsign(ソフトサイン関数)
softsignは入力が大きいと1に収束し、入力が小さくなると-1に収束するような関数です。
-1から1の間の入力に対しての変化には敏感になっています。
$$f(x)=\frac{x}{1+|x|}$$
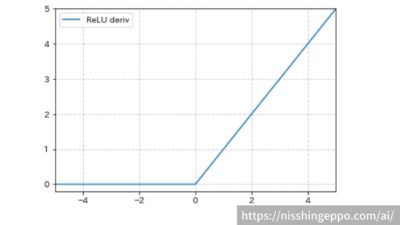
ReLU(ランプ関数)
ReLUは入力が0以上の場合にはそのまま出力され、入力が0以下の場合には0が出力される関数です。
正の入力に対しての変化のみに着目し、負の入力に対する変化は無視しています。
現在最も利用されている活性化関数だと思います。
$$
f(x)=max(0,x)= \begin{cases}
x & (0 \le x) \\
-x & (x < 0)
\end{cases}
$$
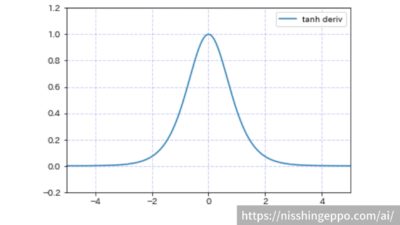
tanh(双曲線関数)
tanhは入力の絶対値が大きい場合に0に収束し、入力が0に近づくと出力が1に近づく関数です。
-2から2の間の入力に対する変化に着目していますが、正負の関係には影響を受けません。
$$f(x)=tanh(x)=\frac{e^{-x}-e^{x}}{e^{-x}+e^{x}}$$
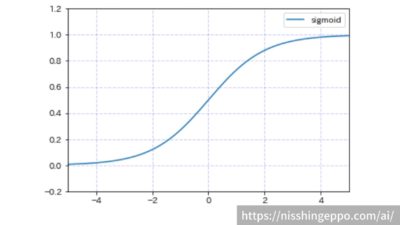
sigmoid(シグモイド関数)
sigmoidは入力が大きくなると1に収束し、入力が小さくなると0に収束する関数です。
-2から2の間の入力に対する変化に着目した関数です。
$$f(x)=\frac{1}{1+e^{-x}}$$
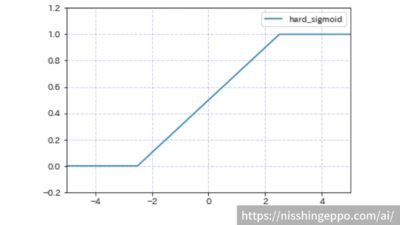
hard_sigmoid(ハードシグモイド関数)
sigmoidは入力が大きくなると1に収束し、入力が小さくなると0に収束する関数です。
-2から2の間の入力に対する変化に対して線形に出力した関数です。
$$f(x)=\begin{cases}1 & (2.5 < x) \\0.2x+0.5(e^{x}-1) & (-2.5 \le x \le 2.5)\\0 & (x < -2.5)\end{cases}$$
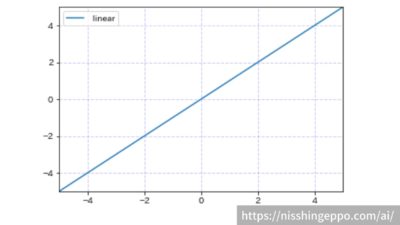
linear(恒等関数)
linerは入力をそのまま出力する関数です。
$$f(x)=x$$





















コメント